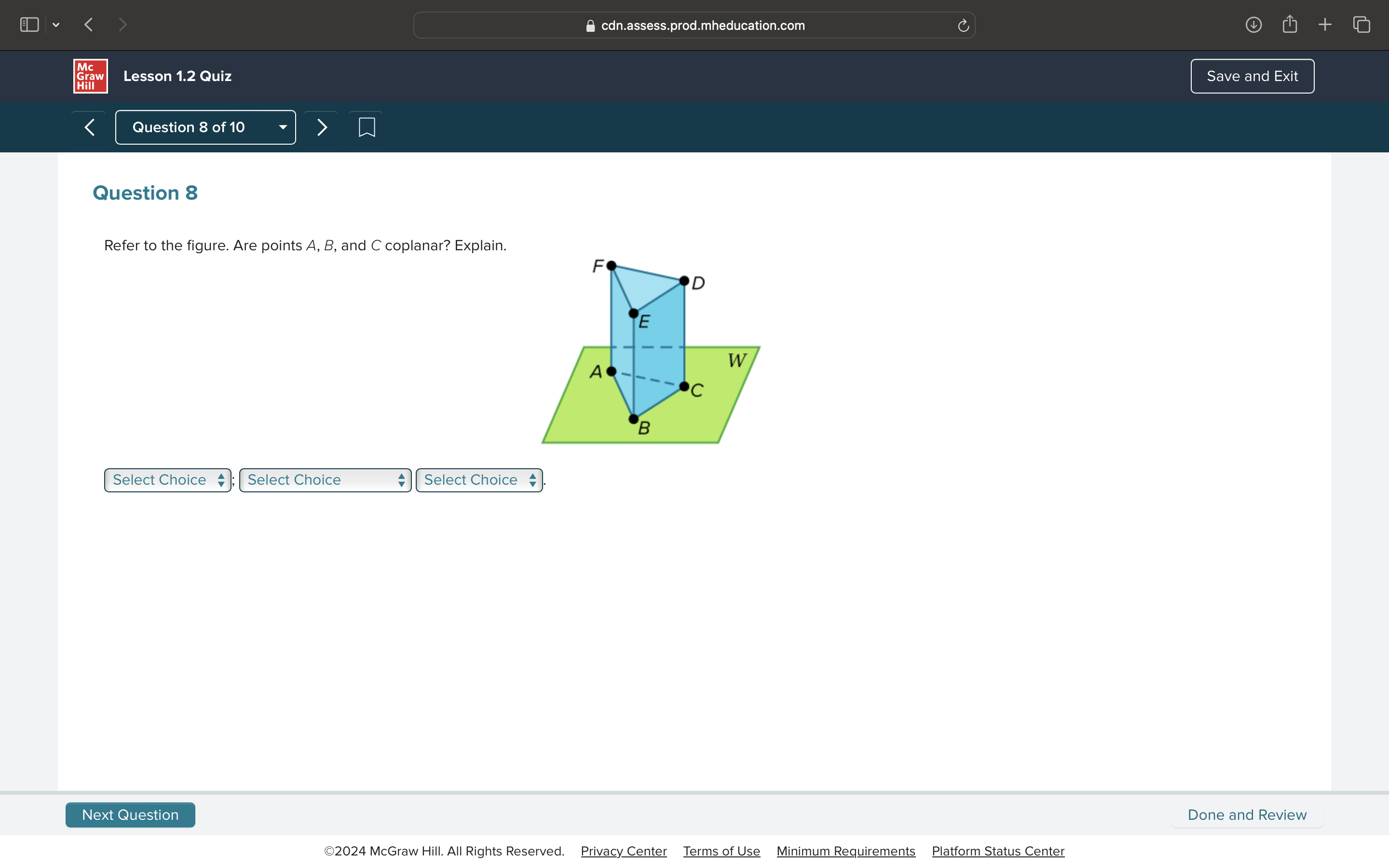
Refer to the figure. Are points A, B, and C coplanar? Explain.
Understand the Problem
The question is asking if the points A, B, and C are coplanar, referring to a geometric figure. To determine if points are coplanar, we will analyze their positions and relations within the figure provided.
Answer
Yes, points A, B, and C are coplanar as they lie on plane W.
Answer for screen readers
Yes, points A, B, and C are coplanar because they all lie on the same plane W.
Steps to Solve
-
Identify the Points and Their Locations
Points A, B, and C are located on plane W, which is represented by the green region in the figure. -
Understanding Coplanarity
Three points are considered coplanar if they lie on the same plane. Since points A, B, and C are all on the same plane W, they are inherently coplanar. -
Conclusion about the Relationship
Since all three points A, B, and C are situated in the same plane, it can be concluded that they are coplanar.
Yes, points A, B, and C are coplanar because they all lie on the same plane W.
More Information
In geometry, points that are coplanar can be visualized as lying on the same flat surface. In this case, since points A, B, and C are on the green plane W, they satisfy the condition for coplanarity.
Tips
- Confusing coplanar points with non-coplanar points in three-dimensional figures. Remember to check their locations carefully.
AI-generated content may contain errors. Please verify critical information