R = √(P² + Q² + 2PQ cosθ) के नियम से हल करें। दो बल P = 5N, Q = 12N, R = 13N हैं।
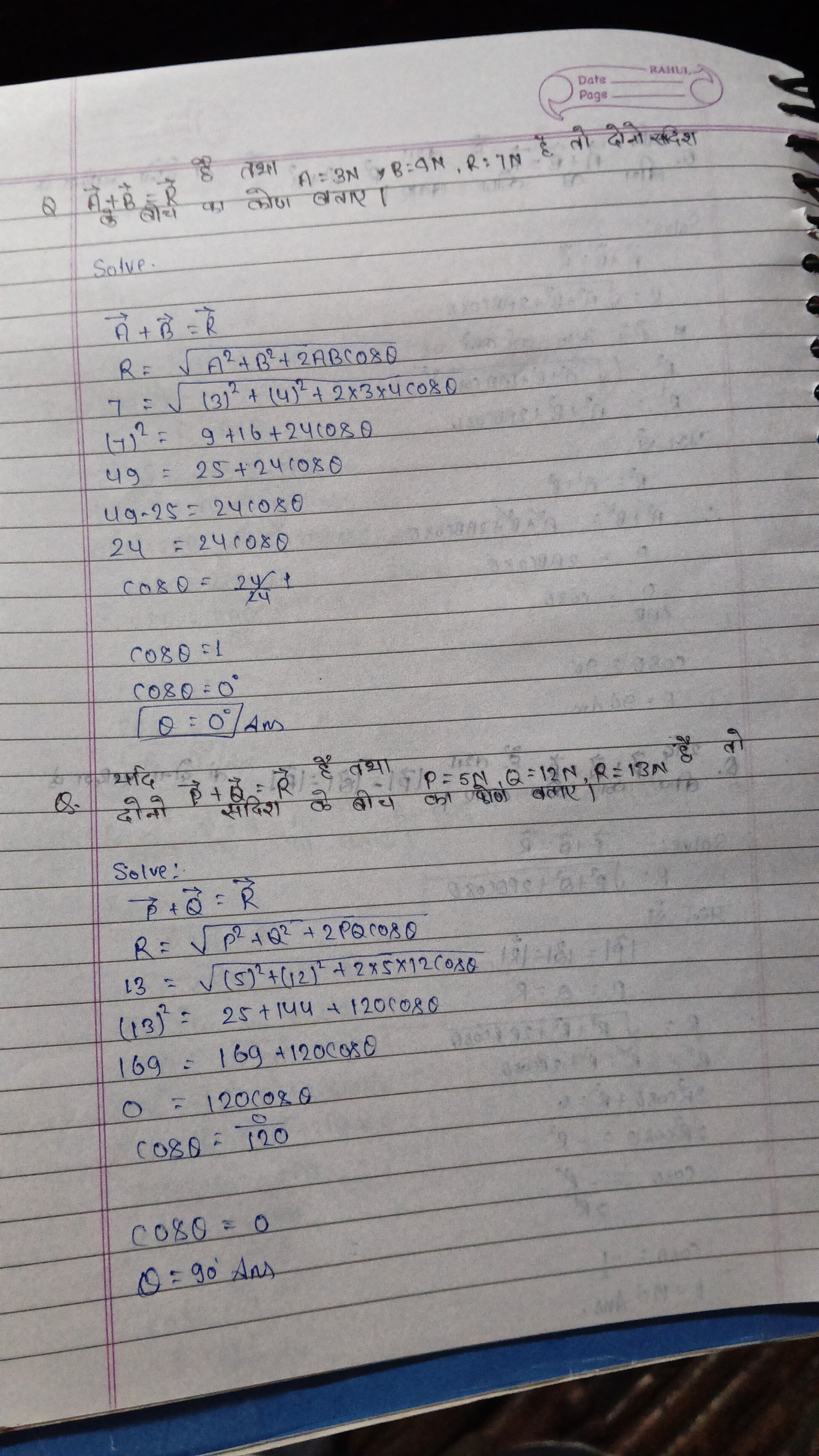
Understand the Problem
यह प्रश्न रेखीय शक्ति और कोसाइन के नियम से संबंधित है। इसे हल करने के लिए, हमें दिए गए भौतिक माप और त्रिकोणमिति का उपयोग करना होगा। प्रश्न में दो बलों के जोड़ को निकालने की प्रक्रिया दिखाई गई है, और अंतिम उत्तर को निर्धारित करने के लिए विभिन्न गणनाएँ की गई हैं।
Answer
The angle is \( \theta = 90^\circ \).
Answer for screen readers
The angle ( \theta ) is ( 90^\circ ).
Steps to Solve
- Start with the Law of Cosines Equation
The law of cosines is given by:
$$ R = \sqrt{P^2 + Q^2 + 2PQ \cos \theta} $$
Substituting the given values ( P = 5 , N ), ( Q = 12 , N ), ( R = 13 , N ):
$$ 13 = \sqrt{5^2 + 12^2 + 2 \cdot 5 \cdot 12 \cos \theta} $$
- Square Both Sides of the Equation
To eliminate the square root, square both sides:
$$ 169 = 25 + 144 + 120 \cos \theta $$
- Combine Like Terms
Combine ( 25 ) and ( 144 ):
$$ 169 = 169 + 120 \cos \theta $$
- Isolate the Cosine Term
Subtract ( 169 ) from both sides to isolate the cosine term:
$$ 0 = 120 \cos \theta $$
- Solve for Cosine
Divide both sides by ( 120 ):
$$ \cos \theta = 0 $$
- Determine the Angle
Using the properties of cosine, we find:
$$ \theta = 90^\circ $$
The angle ( \theta ) is ( 90^\circ ).
More Information
The solution shows that when two forces are perpendicular to each other, the cosine of the angle between them is zero, leading to the conclusion that the forces are at a right angle.
Tips
- Forgetting to square the terms: When squaring both sides, ensure all components are squared.
- Not isolating terms correctly: Make sure to isolate the cosine term step-by-step to avoid mistakes.
AI-generated content may contain errors. Please verify critical information