Put the quadratic into vertex form and state the coordinates of the vertex: y = x² + 4x + 9.
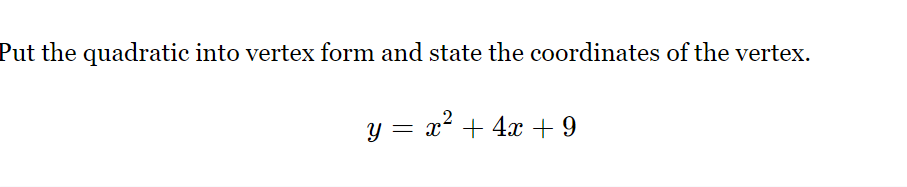
Understand the Problem
The question is asking to convert the given quadratic equation into its vertex form and to identify the coordinates of the vertex. This involves completing the square for the given quadratic equation.
Answer
The vertex form is $y = (x + 2)^2 + 5$ and the vertex coordinates are $(-2, 5)$.
Answer for screen readers
The vertex form of the quadratic equation is $$ y = (x + 2)^2 + 5 $$ and the coordinates of the vertex are $$ (-2, 5) $$.
Steps to Solve
- Identify the quadratic equation
The given quadratic equation is $$ y = x^2 + 4x + 9 $$
- Complete the square
To complete the square, take the coefficient of $x$, which is $4$, divide it by $2$, and square it:
- Coefficient: $4$
- Half: $2$
- Square: $2^2 = 4$
Now rewrite the equation, adding and subtracting this square (4) inside the equation:
$$ y = (x^2 + 4x + 4) + 9 - 4 $$
- Rewrite the equation in vertex form
Now, factor the perfect square trinomial:
$$ y = (x + 2)^2 + 5 $$
This is now in vertex form $y = a(x - h)^2 + k$ where the vertex $(h, k)$ is:
- Identify the vertex coordinates
By comparing the vertex form $(x + 2)^2 + 5$, we see that:
- $h = -2$
- $k = 5$
Thus, the vertex coordinates are $$ (-2, 5) $$
The vertex form of the quadratic equation is $$ y = (x + 2)^2 + 5 $$ and the coordinates of the vertex are $$ (-2, 5) $$.
More Information
The vertex form of a quadratic function provides insight into its graph, showing where it reaches its maximum or minimum. The vertex is crucial for understanding the shape and direction of the parabola represented by the quadratic equation.
Tips
- Forgetting to balance the equation when adding and subtracting the square.
- Incorrectly factoring the perfect square trinomial.
- Misidentifying the vertex coordinates; remember $h$ is negated in $(x - h)$.
AI-generated content may contain errors. Please verify critical information