Provide the integral that represents the area of the region that lies inside r = 3 sin(θ) and outside r = 1 + sin(θ).
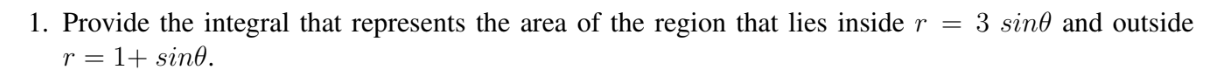
Understand the Problem
The question is asking for the integral that represents the area of a region defined by two polar curves: one lies inside the curve given by r = 3 sin(θ) and the other is represented by r = 1 + sin(θ). We need to set up the appropriate integral to find this area.
Answer
$$ A = \frac{1}{2} \int_{\frac{\pi}{6}}^{\frac{5\pi}{6}} \left( (3 \sin(\theta))^2 - (1 + \sin(\theta))^2 \right) d\theta $$
Answer for screen readers
The integral that represents the area is: $$ A = \frac{1}{2} \int_{\frac{\pi}{6}}^{\frac{5\pi}{6}} \left( (3 \sin(\theta))^2 - (1 + \sin(\theta))^2 \right) d\theta $$
Steps to Solve
-
Identify the curves The given polar curves are ( r = 3 \sin(\theta) ) and ( r = 1 + \sin(\theta) ). We need to find their points of intersection to set the bounds for integration.
-
Find points of intersection To find where the curves intersect, set them equal to each other: $$ 3 \sin(\theta) = 1 + \sin(\theta) $$ This simplifies to: $$ 2 \sin(\theta) = 1 \quad \Rightarrow \quad \sin(\theta) = \frac{1}{2} $$ The solutions for ( \theta ) are ( \theta = \frac{\pi}{6} ) and ( \theta = \frac{5\pi}{6} ).
-
Set up the integral The area ( A ) between the curves in polar coordinates is given by: $$ A = \frac{1}{2} \int_{\alpha}^{\beta} \left( R^2 - r^2 \right) d\theta $$ where ( R ) is the outer curve and ( r ) is the inner curve. Here, ( R = 3 \sin(\theta) ) and ( r = 1 + \sin(\theta) ).
-
Determine the bounds Using the points of intersection, we set the bounds as ( \theta = \frac{\pi}{6} ) to ( \theta = \frac{5\pi}{6} ).
-
Write the complete integral Thus, the integral for the area is: $$ A = \frac{1}{2} \int_{\frac{\pi}{6}}^{\frac{5\pi}{6}} \left( (3 \sin(\theta))^2 - (1 + \sin(\theta))^2 \right) d\theta $$
The integral that represents the area is: $$ A = \frac{1}{2} \int_{\frac{\pi}{6}}^{\frac{5\pi}{6}} \left( (3 \sin(\theta))^2 - (1 + \sin(\theta))^2 \right) d\theta $$
More Information
This integral calculates the area of the region bounded by the two polar curves. The ( \frac{1}{2} ) factor arises from the formula for the area in polar coordinates.
Tips
- Misidentifying outer and inner curves: Make sure to correctly identify which curve is outside and which is inside based on the angle ( \theta ).
- Incorrect bounds: Ensure you find all points of intersection; missing one can lead to incorrect integration limits.
AI-generated content may contain errors. Please verify critical information