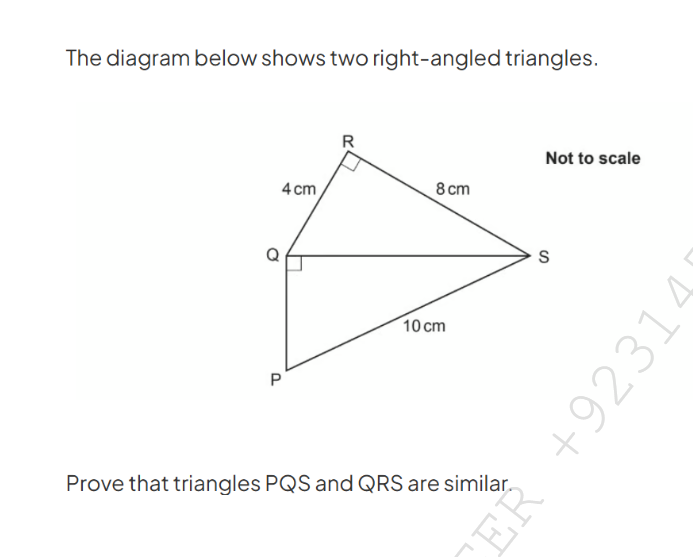
Prove that triangles PQS and QRS are similar.
Understand the Problem
The question is asking to prove that triangles PQS and QRS are similar based on their angles and side lengths. To solve this, we will likely use the criteria for triangle similarity, such as AA (Angle-Angle) or the property of proportional sides.
Answer
Triangles \( \triangle PQS \) and \( \triangle QRS \) are similar by the AA similarity criterion.
Answer for screen readers
The triangles ( \triangle PQS ) and ( \triangle QRS ) are similar by AA similarity criterion.
Steps to Solve
-
Identify the right angles Both triangles PQS and QRS have right angles at points Q and R respectively. Thus, we know that angle (PQRS) and angle (QRS) are both (90^\circ).
-
Use the property of angles Since triangle PQS and triangle QRS share angle QRS, we can say that:
- ( \angle PQS = \angle QRS ) since they are corresponding angles.
- Conclusion about the angles By the AA (Angle-Angle) similarity criterion, we find that:
- ( \angle PQS + 90^\circ = \angle QRS + 90^\circ ) implies both triangles share two angles.
- Apply triangle similarity So, by AA similarity criterion:
- ( \triangle PQS \sim \triangle QRS )
The triangles ( \triangle PQS ) and ( \triangle QRS ) are similar by AA similarity criterion.
More Information
Triangles are similar when they have the same shape, even if the size is different. The AA similarity criterion states that if two angles of one triangle are equal to the two angles of another triangle, then the triangles are similar.
Tips
null
AI-generated content may contain errors. Please verify critical information