Prove that A - B = A ∩ B' where A and B are arbitrary sets.
Understand the Problem
The question is asking to prove the equality between the set difference A - B and the intersection of set A with the complement of set B. It involves applying set theory principles to demonstrate this equality.
Answer
The equality is \( A - B = A \cap B' \).
Answer for screen readers
The proof shows that ( A - B = A \cap B' ).
Steps to Solve
- Define the Left-Hand Side (LHS)
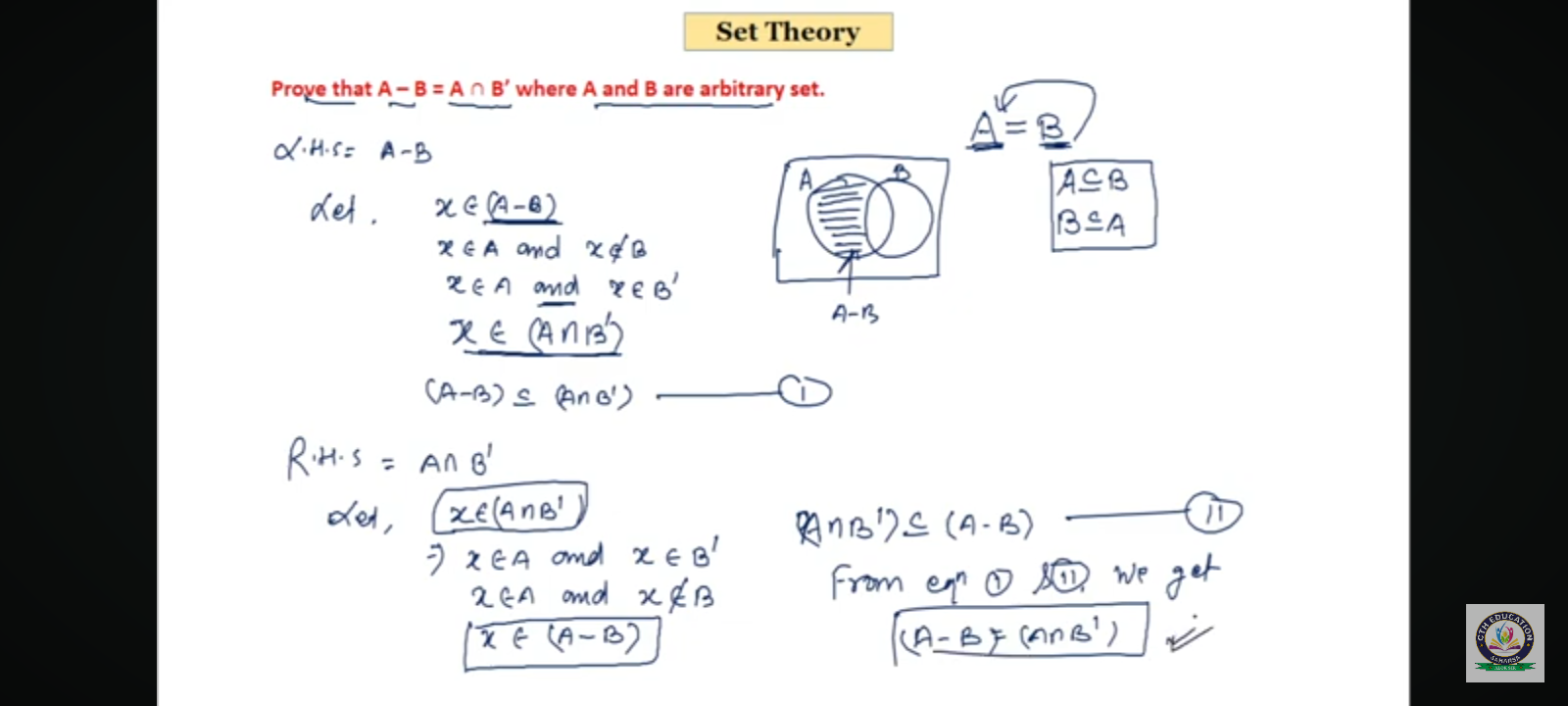
The left-hand side of the equation is given as $A - B$. We can define an element $x$ that belongs to this set: $$ x \in (A - B) \implies x \in A \text{ and } x \notin B $$
- Show LHS is a subset of RHS
We need to show that $A - B \subseteq (A \cap B')$.
From our definition in step 1: $$ x \in A \text{ and } x \notin B $$ This implies: $$ x \in A \text{ and } x \in B' $$
Therefore, $$ x \in (A \cap B') $$
- Define the Right-Hand Side (RHS)
Now, let's define the right-hand side of the equation, which is $A \cap B'$. Defining an element $x$ that belongs to this set gives us: $$ x \in (A \cap B') \implies x \in A \text{ and } x \in B' $$
- Show RHS is a subset of LHS
This means: $$ x \in A \text{ and } x \notin B $$
Thus, we conclude: $$ x \in (A - B) $$
- Combine the Results
From steps 2 and 4, we have shown both: $$ A - B \subseteq (A \cap B') $$ and $$ A \cap B' \subseteq (A - B) $$
Thus, we can conclude: $$ A - B = (A \cap B') $$
The proof shows that ( A - B = A \cap B' ).
More Information
This equality is a fundamental property in set theory, indicating how the difference of sets can be expressed in terms of intersections and complements.
Tips
- Confusing the definitions of set difference and intersection.
- Misapplying the definitions, especially regarding membership in complements.
AI-generated content may contain errors. Please verify critical information