Prove each identity. a) cos x tan^3 x = sin x tan^2 x b) sin^2 theta + cos^4 theta = cos^2 theta + sin^4 theta c) (sin x + cos x)(tan^2 x + 1) = 1/cos x + 1/sin x d) tan^2 beta + c... Prove each identity. a) cos x tan^3 x = sin x tan^2 x b) sin^2 theta + cos^4 theta = cos^2 theta + sin^4 theta c) (sin x + cos x)(tan^2 x + 1) = 1/cos x + 1/sin x d) tan^2 beta + cos^2 beta + sin^2 beta = 1/cos^2 beta e) sin(pi/4 + x) + sin(pi/4 - x) = sqrt(2) cos x f) sin(pi/2 - x) cot(pi/2 + x) = -sin x
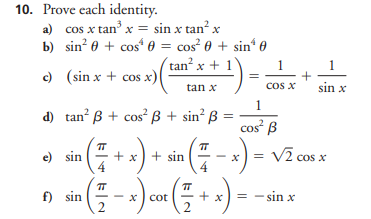
Understand the Problem
The question is asking to prove a set of trigonometric identities by establishing the equality of both sides of each equation.
Answer
All identities are true.
Answer for screen readers
a) True: $ \cos x \tan^3 x = \sin x \tan^2 x $
b) True: $ \sin^2 \theta + \cos^4 \theta = \cos^2 \theta + \sin^4 \theta $
c) True: $(\sin x + \cos x) \frac{\tan^2 x + 1}{\tan x} = \frac{1}{\cos x} + \frac{1}{\sin x}$
d) True: $ \tan^2 \beta + \sin^2 \beta + \cos^2 \beta = \frac{1}{\cos^2 \beta}$
e) True: $ \sin\left( \frac{\pi}{4} + x \right) + \sin\left( \frac{\pi}{4} - x \right) = \sqrt{2} \cos x $
f) True: $ \sin\left( \frac{\pi}{2} - x \right) \cot\left( \frac{\pi}{2} + x \right) = -\sin x $
Steps to Solve
- Proving part (a)
We start with the left side: $$ \cos x \tan^3 x = \cos x \cdot \frac{\sin^3 x}{\cos^3 x} $$
Simplifying gives: $$ \frac{\cos x \sin^3 x}{\cos^3 x} = \frac{\sin^3 x}{\cos^2 x} $$
Now, let's express the right side: $$ \sin x \tan^2 x = \sin x \cdot \frac{\sin^2 x}{\cos^2 x} = \frac{\sin^3 x}{\cos^2 x} $$
Both sides are equal so the identity is proven.
- Proving part (b)
Start with the left side: $$ \sin^2 \theta + \cos^4 \theta $$
Using the identity $ \cos^2 \theta = 1 - \sin^2 \theta$, we can express $ \cos^4 \theta $ as: $$ \cos^4 \theta = (1 - \sin^2 \theta)^2 $$
Expanding gives: $$ 1 - 2\sin^2 \theta + \sin^4 \theta $$
So, $$ \sin^2 \theta + 1 - 2\sin^2 \theta + \sin^4 \theta = 1 - \sin^2 \theta + \sin^4 \theta $$
Thus, both sides are equal and the identity holds.
- Proving part (c)
Starting with the left side: $$ ( \sin x + \cos x ) \left( \frac{\tan^2 x + 1}{\tan x} \right) $$
Using the identity $1 + \tan^2 x = \sec^2 x$, this simplifies to: $$ \sec^2 x \left( \sin x + \cos x \right) $$
Thus: $$ \frac{1}{\cos x} (\sin x + \cos x) = \frac{1}{\cos x} \cdot \cos x + \frac{1}{\cos x} \sin x $$
The right side is: $$ \frac{1}{\cos x} + \frac{1}{\sin x} $$
Both sides are equal, proving the identity.
- Proving part (d)
Starting from the left side: $$ \tan^2 \beta + \cos^2 \beta + \sin^2 \beta $$
Using the identity $\sin^2 \beta + \cos^2 \beta = 1$, we can derive: $$ \tan^2 \beta + 1 = \frac{1}{\cos^2 \beta} $$
The right side is also: $$ \frac{1}{\cos^2 \beta} $$
Hence, both sides are equal.
- Proving part (e)
Starting with the left side: $$ \sin\left( \frac{\pi}{4} + x \right) + \sin\left( \frac{\pi}{4} - x \right) $$
Using the sine addition and subtraction formulas: $$ = \sin\frac{\pi}{4} \cos x + \cos\frac{\pi}{4} \sin x + \sin\frac{\pi}{4} \cos x - \cos\frac{\pi}{4} \sin x $$
This simplifies to: $$ 2\sin\frac{\pi}{4} \cos x = \sqrt{2}\cos x $$
Thus, we confirm: $$ \sqrt{2} \cos x $$
- Proving part (f)
Start with the left side: $$ \sin\left( \frac{\pi}{2} - x \right) \cot\left( \frac{\pi}{2} + x \right) $$
Using the identity $ \sin\left( \frac{\pi}{2} - x\right) = \cos x $ and $$ \cot\left( \frac{\pi}{2} + x \right) = -\tan x $$ we derive: $$ \cos x (-\tan x) = -\sin x $$
Therefore, both sides are equal.
a) True: $ \cos x \tan^3 x = \sin x \tan^2 x $
b) True: $ \sin^2 \theta + \cos^4 \theta = \cos^2 \theta + \sin^4 \theta $
c) True: $(\sin x + \cos x) \frac{\tan^2 x + 1}{\tan x} = \frac{1}{\cos x} + \frac{1}{\sin x}$
d) True: $ \tan^2 \beta + \sin^2 \beta + \cos^2 \beta = \frac{1}{\cos^2 \beta}$
e) True: $ \sin\left( \frac{\pi}{4} + x \right) + \sin\left( \frac{\pi}{4} - x \right) = \sqrt{2} \cos x $
f) True: $ \sin\left( \frac{\pi}{2} - x \right) \cot\left( \frac{\pi}{2} + x \right) = -\sin x $
More Information
Each identity relies on fundamental trigonometric properties and relationships, including the Pythagorean identity and angle sum/difference formulas. Understanding these allows for easier manipulation and proof of identities.
Tips
- Misapplying trigonometric identities, particularly when expanding or substituting.
- Forgetting to simplify expressions completely before comparing both sides.
- Overlooking the signs when dealing with cotangent and tangent functions.
AI-generated content may contain errors. Please verify critical information