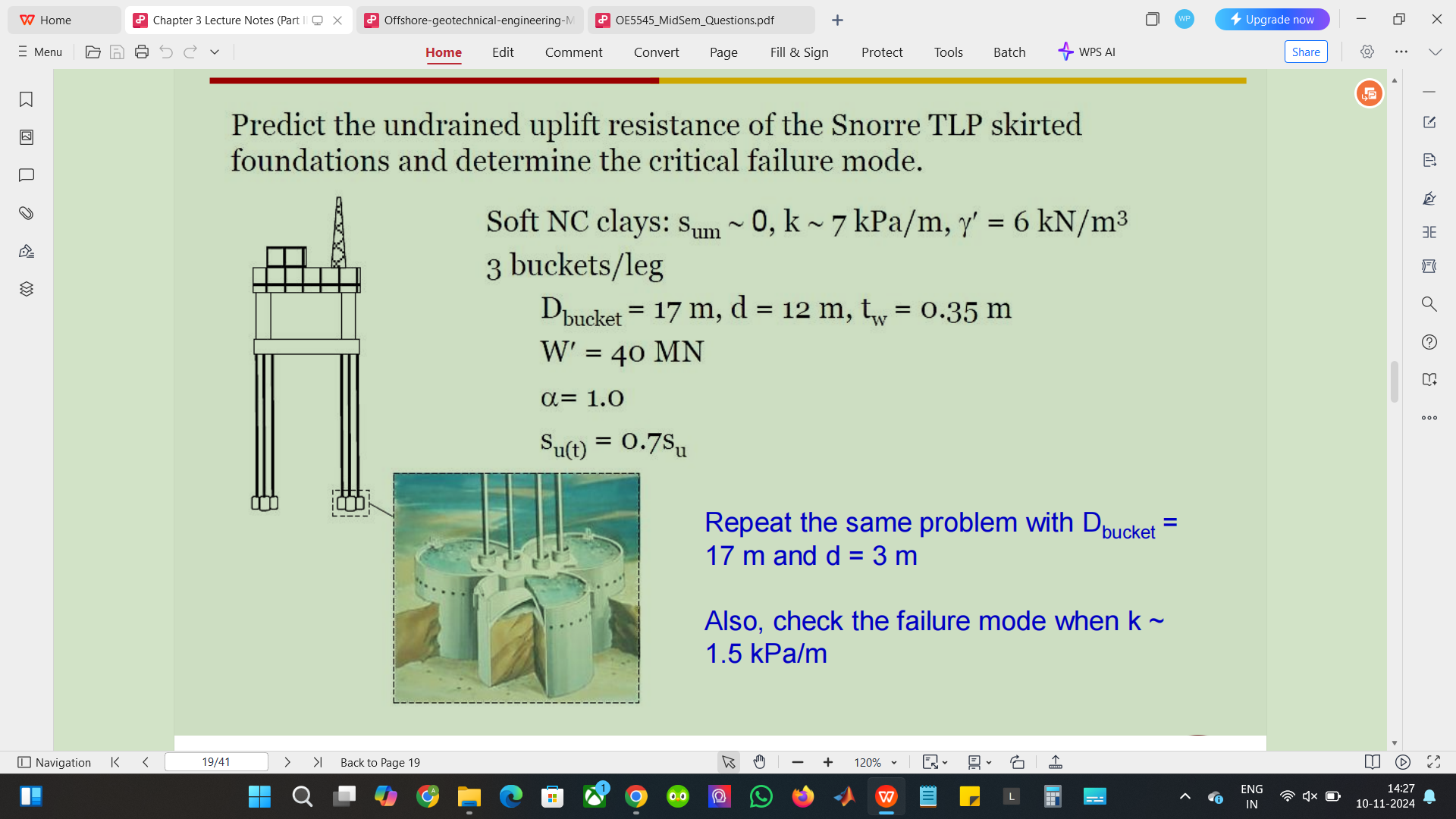
Predict the undrained uplift resistance of the Snorre TLP skirted foundations and determine the critical failure mode. Repeat the same problem with D_bucket = 17 m and d = 3 m. Als... Predict the undrained uplift resistance of the Snorre TLP skirted foundations and determine the critical failure mode. Repeat the same problem with D_bucket = 17 m and d = 3 m. Also, check the failure mode when k = 1.5 kPa/m. Read more

Steps to Solve

1. Calculate Undrained Shear Strength ($s_u$) The undrained shear strength is given by: $$ s_u = s_u(t) = 0.7 \cdot s_u $$ Where $s_u$ is the undrained shear strength parameter. Since $s_u$ is not explicitly given, we need to relate it to other parameters.

2. Determine the Effective Weight of the Foundation The effective weight of the foundation for uplift resistance can be calculated as: $$ W' = 40 , \text{MN} $$

3. Calculate the Area of the Base of Each Bucket The area for one bucket is given by: $$ A = \frac{\pi}{4} D_{\text{bucket}}^2 $$ Using $D_{\text{bucket}} = 17 , \text{m}$, calculate: $$ A = \frac{\pi}{4} \cdot (17 , \text{m})^2 $$

4. Calculate the Total Area for Three Buckets The total area ($A_{total}$) for three buckets is: $$ A_{total} = 3 \cdot A $$

5. Determine Undrained Uplift Resistance ($R_u$) The undrained uplift resistance can be calculated using: $$ R_u = s_u \cdot A_{total} $$ Substitute $s_u$ from step 1 and $A_{total}$ from step 4 to find $R_u$.

6. Identify Critical Failure Mode Analyze the uplift resistance to identify the critical failure mode, whether it's due to soil failure or structural failure. This generally depends on comparing $R_u$ and the effective weight ($W'$).

7. Repeat with Modified Dimensions Repeat steps 3-6 with the modified bucket diameter $D_{\text{bucket}} = 17 , \text{m}$ and a smaller depth $d = 3 , \text{m}$.

8. Check Failure Mode with Different $k$ Value For $k \sim 1.5 , \text{kPa/m}$, repeat the analysis to check for any changes in failure mode.