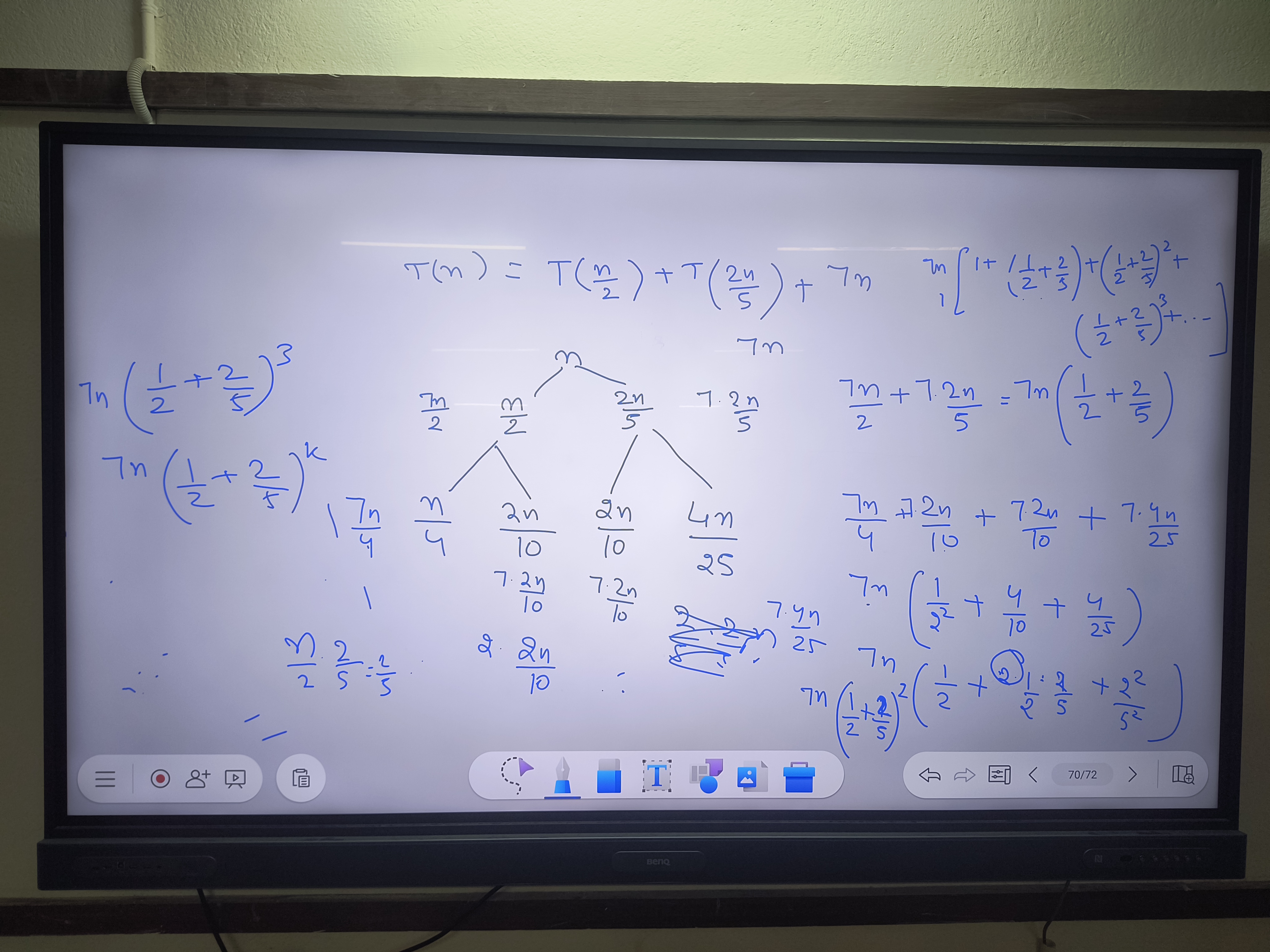
π(m) = T(m/2) + T(2n/5) + 7n (1 + (1/2 + 2/5)² + (1/2 + 2/5)³ + ...)

Steps to Solve

1. Identifying the recursive formula

The function is given as:
$$ \pi(m) = T\left(\frac{m}{2}\right) + T\left(\frac{2n}{5}\right) + 7n \left(1 + \left(\frac{1}{2} + \frac{2}{5}\right)^2 + \left(\frac{1}{2} + \frac{2}{5}\right)^3 + \ldots\right) $$

2. Simplifying the series

The series inside the parentheses is a geometric series. The constant ratio is:
$$ r = \frac{1}{2} + \frac{2}{5} = \frac{5}{10} + \frac{4}{10} = \frac{9}{10} $$
The sum of an infinite geometric series can be calculated using the formula:
$$ S = \frac{a}{1 - r} $$
where ( a ) is the first term, which is 1 in this case.

3. Finding the sum of the series

Substituting ( a = 1 ) and ( r = \frac{9}{10} ):
$$ S = \frac{1}{1 - \frac{9}{10}} = \frac{1}{\frac{1}{10}} = 10 $$

4. Substituting back into the function

Now substitute the series sum back into the original formula:
$$ \pi(m) = T\left(\frac{m}{2}\right) + T\left(\frac{2n}{5}\right) + 7n \cdot 10 $$
Which simplifies to:
$$ \pi(m) = T\left(\frac{m}{2}\right) + T\left(\frac{2n}{5}\right) + 70n $$

5. Exploring the recurrence relation further

If we are solving for ( T ), we would continue to express ( T ) in terms of other ( T ) values until a base case is reached, but this can depend on the additional properties of ( T ) not shown.

6. Final expansion and conclusion

As it stands, the equation describes ( \pi(m) ) with contributions from two different recursive calls to ( T ) and a linear term of ( 70n ). Further analysis would require properties of ( T ).