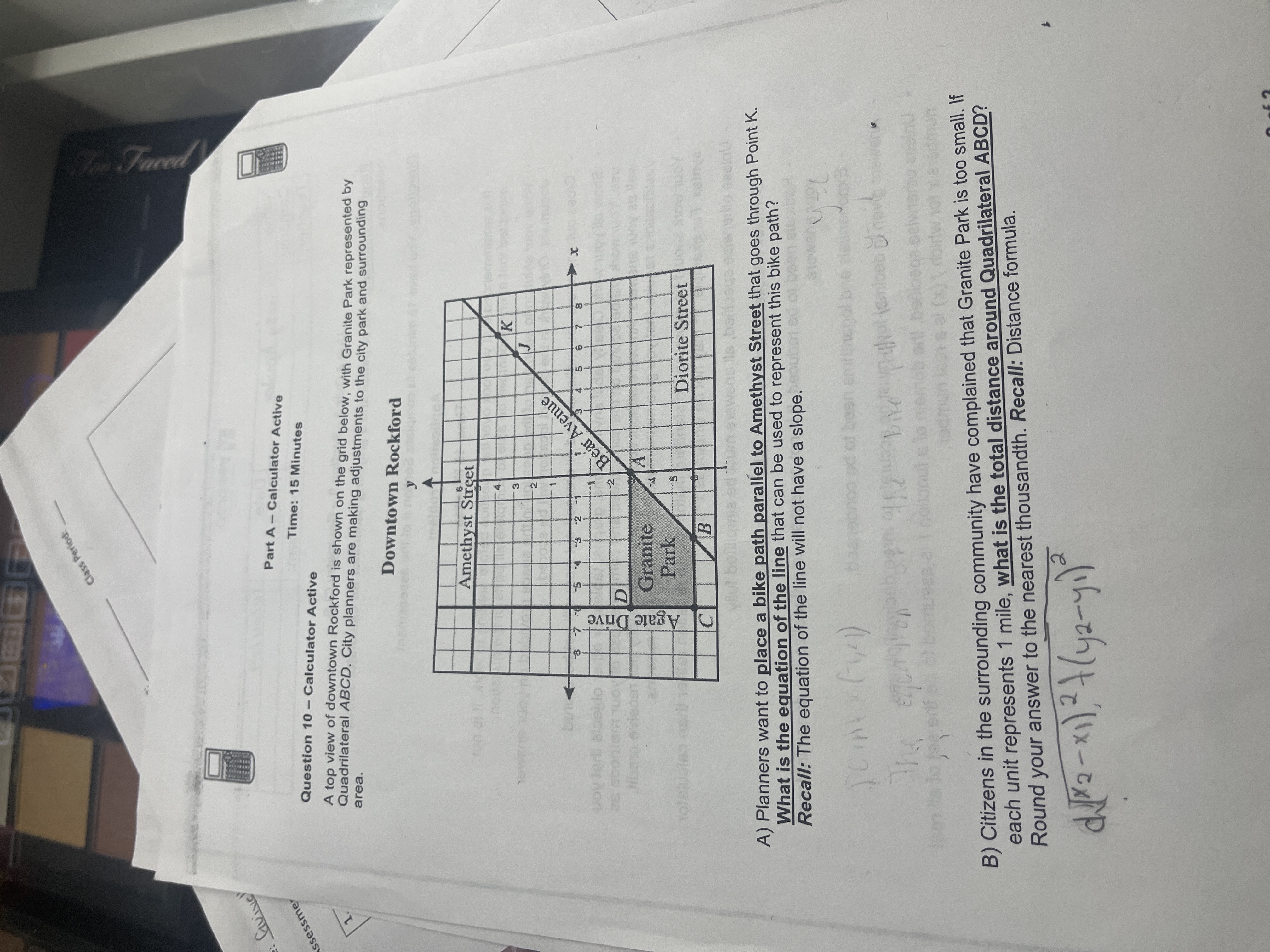
Planners want to place a bike path parallel to Amethyst Street that goes through Point K. What is the equation of the line that can be used to represent this bike path? Recall: The... Planners want to place a bike path parallel to Amethyst Street that goes through Point K. What is the equation of the line that can be used to represent this bike path? Recall: The equation of the line will not have a slope. Citizens in the surrounding community have complained that Granite Park is too small. If each unit represents 1 mile, what is the total distance around Quadrilateral ABCD? Round your answer to the nearest thousandth. Recall: Distance formula.
Understand the Problem
The question consists of two parts: A) It asks for the equation of a line parallel to Amethyst Street that goes through a specific point. B) It asks for the total distance around a quadrilateral given that each unit on the grid represents one mile, requiring the application of the distance formula.
Answer
A) $y = k$ B) Total distance = sum of lengths of sides ABCD in miles.
Answer for screen readers
A) The equation of the line parallel to Amethyst Street that goes through Point K is $y = k$, where $k$ is the y-coordinate of Point K.
B) The total distance around Quadrilateral ABCD is calculated using the coordinates of points A, B, C, and D, which needs to be summed up based on the calculated lengths.
Steps to Solve
- Determine the slope of Amethyst Street
Amethyst Street is represented as a horizontal line on the grid. Since it's horizontal, its slope is $0$.
- Write the equation of a horizontal line
The equation of a line with a slope of $0$ in the form $y = mx + b$ simplifies to just $y = c$, where $c$ is a constant. For a line parallel to Amethyst Street passing through a point, say Point K (which should have coordinates provided in the grid), the equation will be of the form:
$$ y = k $$
where $k$ is the y-coordinate of Point K.
- Find the vertices of Quadrilateral ABCD
Identify the coordinates of points A, B, C, and D from the grid to calculate the distances accurately.
- Apply the distance formula for each side of Quadrilateral ABCD
Using the distance formula:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
Calculate the length of each side (AB, BC, CD, DA) using the coordinates of the points.
- Sum the lengths to find the total distance
Add the distances of the four sides:
$$ \text{Total Distance} = AB + BC + CD + DA $$
A) The equation of the line parallel to Amethyst Street that goes through Point K is $y = k$, where $k$ is the y-coordinate of Point K.
B) The total distance around Quadrilateral ABCD is calculated using the coordinates of points A, B, C, and D, which needs to be summed up based on the calculated lengths.
More Information
For part A, the horizontal line equation indicates that the bike path maintains the same vertical position as Point K. For part B, the total distance calculation ensures planners have a clear understanding of the perimeter of the quadrilateral area in miles.
Tips
- Incorrect slope calculation: Remember that horizontal lines have a slope of $0$.
- Forgetting to sum all sides: Ensure all side lengths are calculated and added together for the total distance.
