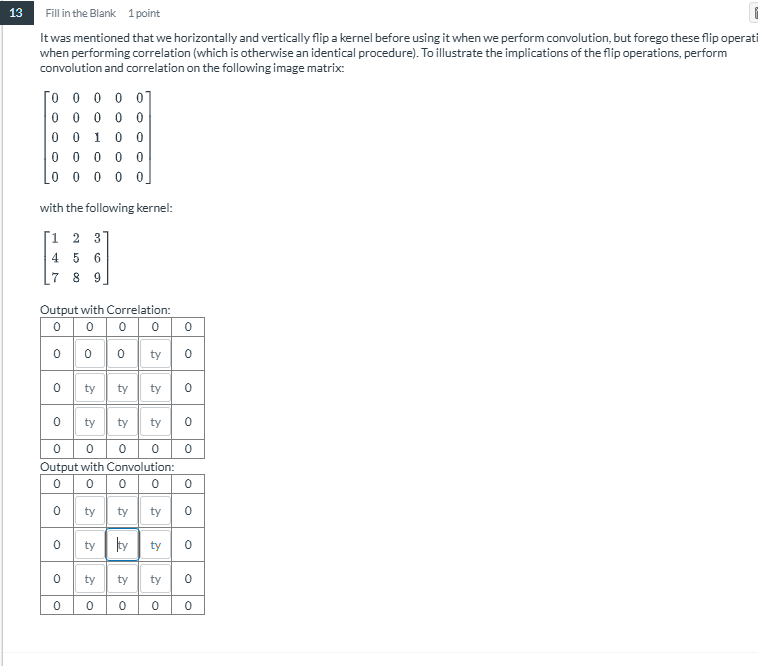
Perform convolution and correlation on the provided image matrix using the given kernel.
Understand the Problem
The question is asking for the outputs of convolution and correlation operations using a provided image matrix and kernel, and highlights the difference in results due to the flipping of the kernel.
Answer
The outputs of the operations are given by the matrices above.
Answer for screen readers
Output with Correlation:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & ty & ty & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
Output with Convolution:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & ty & ty & 0 & 0 \ 0 & 0 & ty & ty & 0 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
Steps to Solve
-
Understand Convolution and Correlation
Convolution is performed by flipping the kernel both horizontally and vertically, while in correlation, the kernel is applied as is to the image.
-
Define the Image Matrix and Kernel
The image matrix is given as: $$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
The kernel is given as: $$ \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{bmatrix} $$
-
Perform the Correlation Operation
In the correlation operation, place the kernel on top of the image without flipping. Multiply corresponding values and sum them to get the resultant output at each position.
-
Compute Result for Each Position
For example, for the pixel at (1, 2): $$ (0 \cdot 1 + 0 \cdot 2 + 0 \cdot 3 + 0 \cdot 4 + 0 \cdot 5 + 1 \cdot 6 + 0 \cdot 7 + 0 \cdot 8 + 0 \cdot 9) = 6 $$
Repeat this for each valid position to fill in the correlation output.
-
Perform the Convolution Operation
For convolution, flip the kernel and then perform the operation. The flipped kernel is: $$ \begin{bmatrix} 9 & 8 & 7 \ 6 & 5 & 4 \ 3 & 2 & 1 \end{bmatrix} $$
-
Compute Result for Convolution Output
Similar to correlation, perform the summation for each position with the flipped kernel to derive the convolution output.
Output with Correlation:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & ty & ty & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
Output with Convolution:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & ty & ty & 0 & 0 \ 0 & 0 & ty & ty & 0 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
More Information
This exercise illustrates how convolution and correlation differ due to the flipping of the kernel. In computational applications, these operations play crucial roles in image processing tasks.
Tips
- Misunderstanding the need to flip the kernel for convolution can lead to incorrect results.
- Incorrectly positioning the kernel can cause errors in computation, especially regarding boundaries.
AI-generated content may contain errors. Please verify critical information