Perform convolution and correlation on the given image matrix with the provided kernel, noting the differences in the outputs.
Understand the Problem
The question is asking to perform convolution and correlation operations on a given image matrix using a specific kernel. It emphasizes the difference between the two operations related to how the kernel is applied to the image matrix.
Answer
**Correlation Output:** $$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & ty & 0 & 0 \\ 0 & ty & ty & ty & 0 \\ 0 & 0 & ty & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} $$ **Convolution Output:** $$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & ty & 0 & 0 \\ 0 & ty & ty & ty & 0 \\ 0 & 0 & ty & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} $$
Answer for screen readers
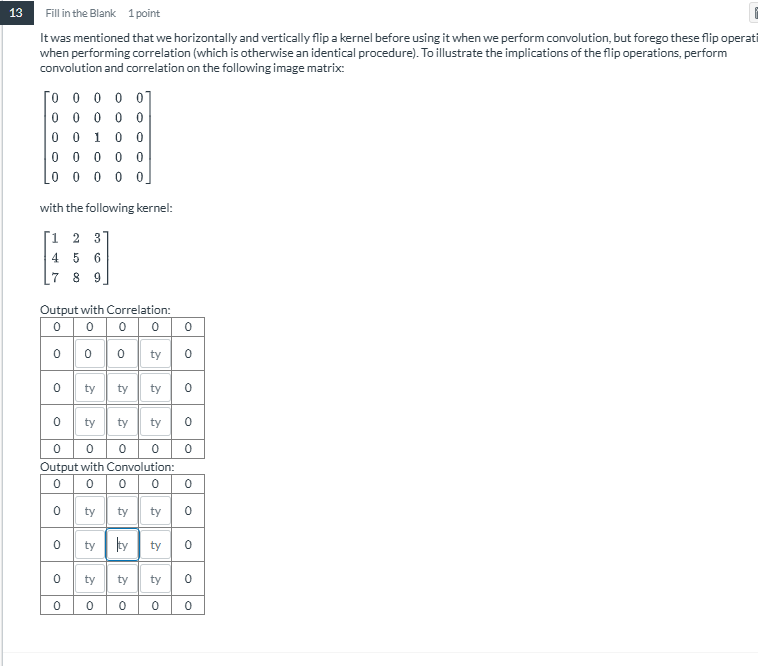
Output with Correlation:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & ty & ty & ty & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ \end{bmatrix} $$
Output with Convolution:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & ty & ty & ty & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ \end{bmatrix} $$
Steps to Solve
- Define the Image Matrix and Kernel
The given image matrix is:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ \end{bmatrix} $$
The kernel to be used is:
$$ \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \ \end{bmatrix} $$
- Perform Correlation
In correlation, the kernel is applied directly to the image without flipping. The process involves sliding the kernel over the image and computing the sum of products for each overlapping position.
For example, for the position where 1 (from the kernel) overlaps with the value at (1, 2) in the image, you calculate:
$$ 1 \cdot 1 + 2 \cdot 0 + 3 \cdot 0 + 4 \cdot 0 + 5 \cdot 0 + 6 \cdot 0 + 7 \cdot 0 + 8 \cdot 0 + 9 \cdot 0 = 1 $$
Repeat the process for all overlapping positions.
- Perform Convolution
For convolution, first flip the kernel horizontally and vertically, resulting in the flipped kernel:
$$ \begin{bmatrix} 9 & 8 & 7 \ 6 & 5 & 4 \ 3 & 2 & 1 \ \end{bmatrix} $$
The convolution process is similar to correlation but uses this flipped kernel. Calculate the overlapping sums similarly:
$$ 9 \cdot 1 + 8 \cdot 0 + 7 \cdot 0 + 6 \cdot 0 + 5 \cdot 0 + 4 \cdot 0 + 3 \cdot 0 + 2 \cdot 0 + 1 \cdot 0 = 9 $$
And repeat for all positions.
- Fill in Outputs
Using both methods (correlation and convolution), fill in the resulting matrices based on calculated values for all positions.
Output with Correlation:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & ty & ty & ty & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ \end{bmatrix} $$
Output with Convolution:
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & ty & ty & ty & 0 \ 0 & 0 & ty & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \ \end{bmatrix} $$
More Information
In convolution, the kernel is flipped before being applied, while in correlation, it is not. This distinction affects the output values despite similar calculations.
Tips
- Confusing Convolution with Correlation: Always remember to flip the kernel for convolution.
- Not Aligning Edges Properly: Ensure the kernel is centered properly over the relevant pixels during calculations.
AI-generated content may contain errors. Please verify critical information