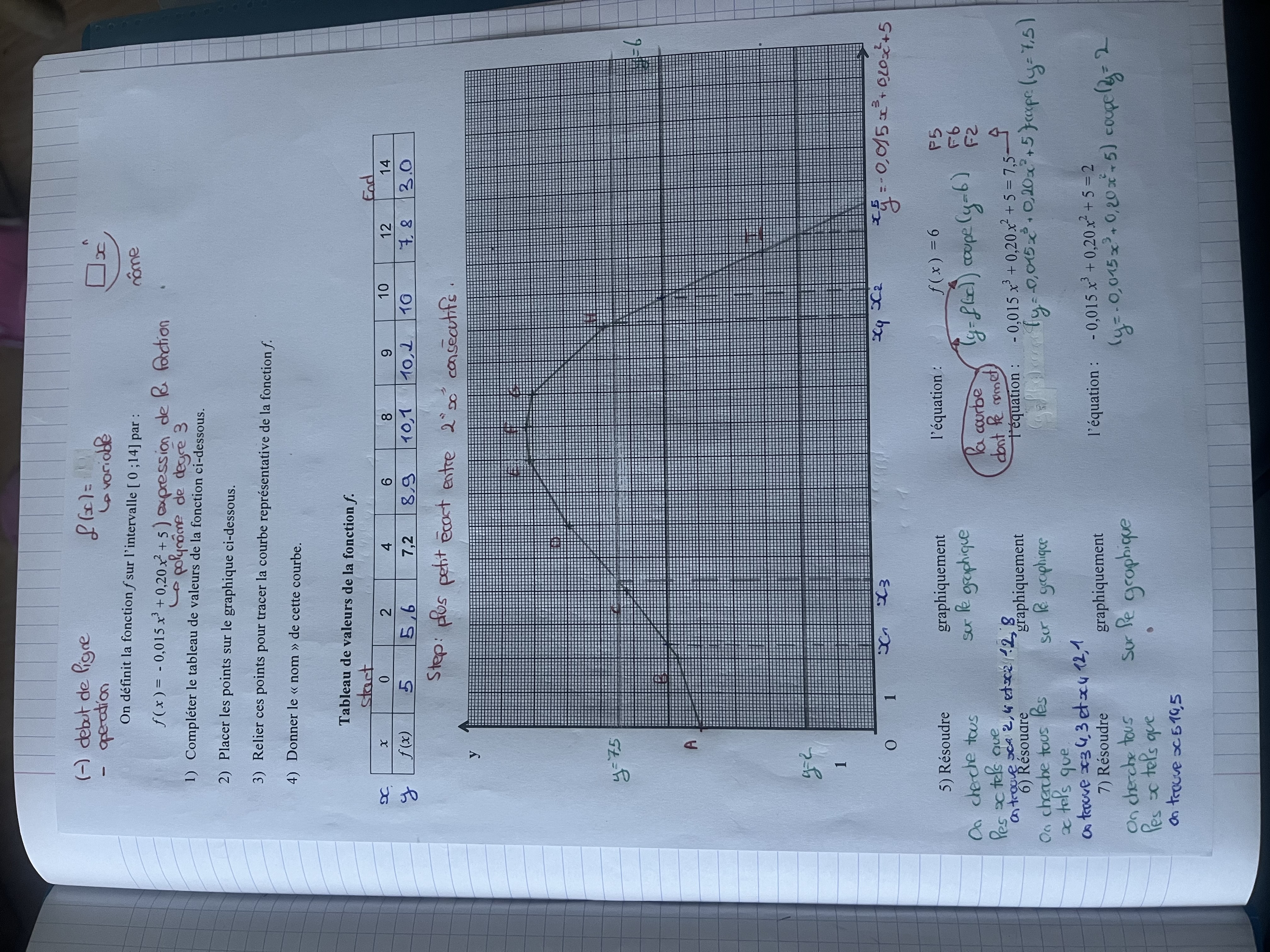
On définit la fonction f sur l'intervalle [0;14] par : f(x) = -0,015 x^3 + 0,20 x^2 + 5. Compléter le tableau de valeurs de la fonction ci-dessous. Placer les points sur le graphiq... On définit la fonction f sur l'intervalle [0;14] par : f(x) = -0,015 x^3 + 0,20 x^2 + 5. Compléter le tableau de valeurs de la fonction ci-dessous. Placer les points sur le graphique ci-dessous. Relier ces points pour tracer la courbe représentative de la fonction f. Donner le nom de cette courbe.
Understand the Problem
La question concerne la définition d'une fonction sur un intervalle, l'analyse de ses valeurs et la représentation graphique. Il s'agit d'un exercice sur les polynômes, impliquant la complétion d'un tableau de valeurs, le traçage de la courbe, et la résolution de certaines équations graphiquement.
Answer
Pour \( f(x) = 6 \), solutions \( x \approx 2.4 \) et \( x \approx 12.8 \). Pour \( f(x) = 2 \), solution \( x \approx 5.5 \).
Answer for screen readers
Les résultats des équations sont obtenus graphiquement. Pour ( f(x) = 6 ), on trouve les intersections avec ( y = 6 ) à des valeurs approximatives de ( x ) (par exemple ( x \approx 2.4 ) et ( x \approx 12.8 )). Pour ( f(x) = 2 ), les intersections se produisent autour de ( x \approx 5.5 ).
Steps to Solve
-
Définir la fonction
On considère la fonction ( f(x) = -0.015x^3 + 0.02x^2 + 5 ). -
Compléter le tableau de valeurs
Pour chaque valeur de ( x ) dans l'intervalle ([0, 14]), on calcule ( f(x) ). Par exemple :- Pour ( x = 0 ) : ( f(0) = -0.015(0)^3 + 0.02(0)^2 + 5 = 5 )
- Pour ( x = 1 ) : ( f(1) = -0.015(1)^3 + 0.02(1)^2 + 5 = 5.6 )
- Continuer ce processus jusqu'à ( x = 14 ) en suivant la même procédure.
-
Tracer le graphique
Placer les points obtenus du tableau sur un système de coordonnées. Utiliser les coordonnées ( (x, f(x)) ) que vous avez calculées. -
Relier les points
Connecter les points avec une courbe lisse pour obtenir la représentation graphique de la fonction ( f ). -
Déterminer le nom de la courbe
La courbe représentant cette fonction est nommée « courbe de degré 3 » ou « courbe polynomiale ». -
Résoudre graphiquement l'équation ( f(x) = 6 )
Trouver les points où la courbe croise la ligne ( y = 6 ). -
Résoudre graphiquement l'équation ( f(x) = 2 )
Trouver les points où la courbe croise la ligne ( y = 2 ).
Les résultats des équations sont obtenus graphiquement. Pour ( f(x) = 6 ), on trouve les intersections avec ( y = 6 ) à des valeurs approximatives de ( x ) (par exemple ( x \approx 2.4 ) et ( x \approx 12.8 )). Pour ( f(x) = 2 ), les intersections se produisent autour de ( x \approx 5.5 ).
More Information
Cette fonction est un polynôme de degré 3, ce qui signifie qu'elle sera représentée par une courbe en 'S' fermée, ayant potentiellement un maximum et un minimum.
Tips
- Oublier de calculer toutes les valeurs du tableau correctement.
- Ne pas relier les points dans le bon ordre sur le graphique.
- Confondre les valeurs d'intersection lorsque plusieurs solutions existent.
AI-generated content may contain errors. Please verify critical information