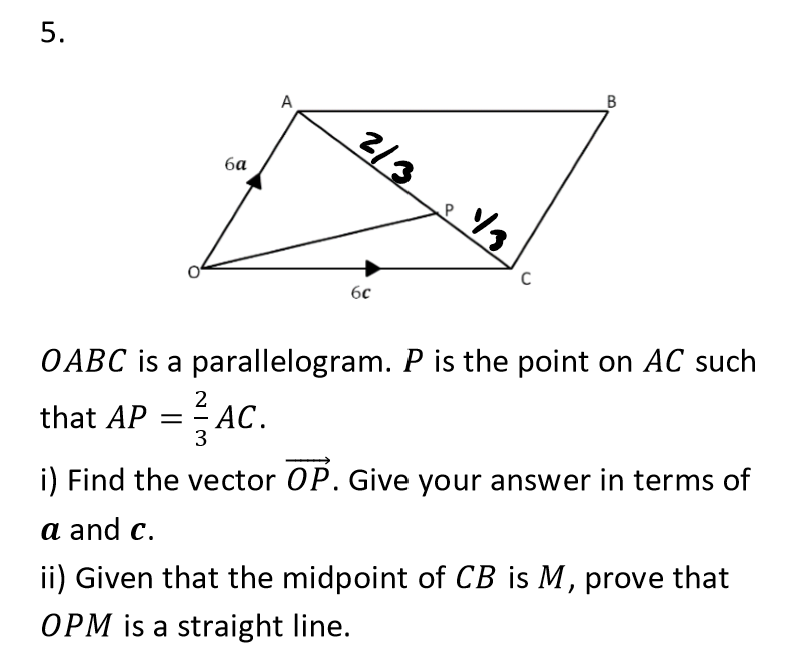
OABC is a parallelogram. P is the point on AC such that AP = 2/3 AC. i) Find the vector OP. Give your answer in terms of a and c. ii) Given that the midpoint of CB is M, prove that... OABC is a parallelogram. P is the point on AC such that AP = 2/3 AC. i) Find the vector OP. Give your answer in terms of a and c. ii) Given that the midpoint of CB is M, prove that OPM is a straight line. Read more

Steps to Solve

1. Identify vectors AC and OP

In a parallelogram, the vector $\overrightarrow{AC}$ can be expressed as the sum of the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$. Using the given vectors: $$ \overrightarrow{AB} = \overrightarrow{6a} $$ $$ \overrightarrow{AC} = \overrightarrow{OB} + \overrightarrow{BC} = \overrightarrow{6a} + \overrightarrow{6c} $$

2. Find vector AC

Using the properties of the parallelogram, we can find that: $$ \overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \overrightarrow{6c} - \overrightarrow{6a} $$

3. Determine point P on AC

Point P divides the segment AC such that: $$ \overrightarrow{AP} = \frac{2}{3} \overrightarrow{AC} $$ Thus, we have: $$ \overrightarrow{OP} = \overrightarrow{OA} + \overrightarrow{AP} = \overrightarrow{6a} + \frac{2}{3} \overrightarrow{AC} $$

4. Substitute AC into OP

Now substituting $\overrightarrow{AC}$ back in gives: $$ \overrightarrow{OP} = \overrightarrow{6a} + \frac{2}{3}(\overrightarrow{6c} - \overrightarrow{6a}) $$

5. Simplify OP

Distributing the $\frac{2}{3}$: $$ \overrightarrow{OP} = \overrightarrow{6a} + \frac{2}{3}\overrightarrow{6c} - \frac{2}{3}\overrightarrow{6a} $$ Combine like terms: $$ \overrightarrow{OP} = \left(6 - \frac{4}{3}\right)\overrightarrow{a} + \frac{4}{3}\overrightarrow{c} $$ $$ \overrightarrow{OP} = \frac{14}{3}\overrightarrow{a} + \frac{4}{3}\overrightarrow{c} $$

6. Prove OPM is a straight line

Given M is the midpoint of CB, we write: $$ \overrightarrow{M} = \frac{1}{2}(\overrightarrow{C} + \overrightarrow{B}) = \frac{1}{2}(\overrightarrow{6c} + \overrightarrow{6a}) = \frac{3}{2}(\overrightarrow{c} + \overrightarrow{a}) $$

7. Check collinearity of O, P, M

For points O, P, and M to be collinear, there must be a scalar $\lambda$ such that: $$ \overrightarrow{OP} = k \overrightarrow{OM} $$

We can express: $$ \overrightarrow{OP} = \frac{14}{3}\overrightarrow{a} + \frac{4}{3}\overrightarrow{c} $$ and $$ \overrightarrow{OM} = \frac{3}{2}(\overrightarrow{c} + \overrightarrow{a}) $$

Thus, verifying if they are proportional will show that they lie on the same line.