Now solving x = A * B
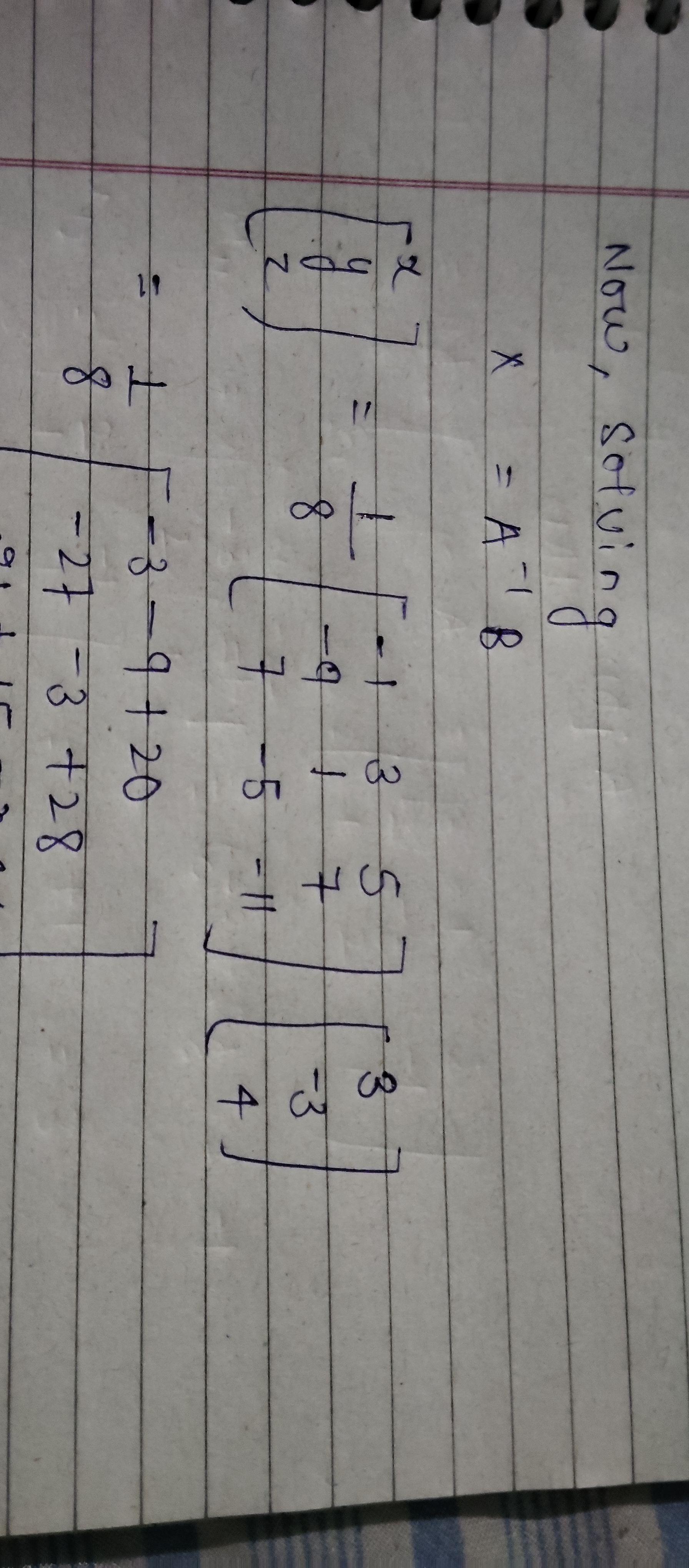
Understand the Problem
The question appears to involve solving a system of linear equations using matrices. It includes manipulation of matrices to find the variable 'x' as part of an equation defined as x = A * B.
Answer
The resulting matrix \( x \) is $$ x = \begin{bmatrix} -26 & 44 \\ -55 & 96 \\ -82 & 149 \end{bmatrix} $$
Answer for screen readers
The resulting matrix ( x ) is:
$$ x = \begin{bmatrix} -26 & 44 \ -55 & 96 \ -82 & 149 \end{bmatrix} $$
Steps to Solve
- Identify Matrix A and Matrix B
From the given information, we can define Matrix A and Matrix B as follows:
$$ A = \begin{bmatrix} 4 & 2 \ 8 & 5 \ 11 & 9 \end{bmatrix}, \quad B = \begin{bmatrix} -5 & 7 \ -3 & 8 \end{bmatrix} $$
- Matrix Multiplication Setup
The multiplication ( x = A * B ) will results in a new matrix ( x ). The resulting matrix ( x ) will have dimensions that correspond to the rows of ( A ) and the columns of ( B ). Thus:
$$ x = \begin{bmatrix} r_1 & r_2 \end{bmatrix} $$ Where ( r_1 ) corresponds to the first row and ( r_2 ) corresponds to the second row of ( x ).
- Perform the Matrix Multiplication
To find the elements of ( x ), we calculate:
$$ x_{ij} = \sum_{k=1}^{n} A_{ik} * B_{kj} $$
Calculating each element:
- First element ( x_{11} ):
$$ x_{11} = (4 \cdot -5) + (2 \cdot -3) = -20 - 6 = -26 $$
- Second element ( x_{12} ):
$$ x_{12} = (4 \cdot 7) + (2 \cdot 8) = 28 + 16 = 44 $$
- Third element ( x_{21} ):
$$ x_{21} = (8 \cdot -5) + (5 \cdot -3) = -40 - 15 = -55 $$
- Fourth element ( x_{22} ):
$$ x_{22} = (8 \cdot 7) + (5 \cdot 8) = 56 + 40 = 96 $$
- Fifth element ( x_{31} ):
$$ x_{31} = (11 \cdot -5) + (9 \cdot -3) = -55 - 27 = -82 $$
- Sixth element ( x_{32} ):
$$ x_{32} = (11 \cdot 7) + (9 \cdot 8) = 77 + 72 = 149 $$
- Construct the Resulting Matrix
Now that we have all elements, we can construct the resulting matrix ( x ):
$$ x = \begin{bmatrix} -26 & 44 \ -55 & 96 \ -82 & 149 \end{bmatrix} $$
The resulting matrix ( x ) is:
$$ x = \begin{bmatrix} -26 & 44 \ -55 & 96 \ -82 & 149 \end{bmatrix} $$
More Information
The matrix multiplication process is essential in linear algebra for solving systems of equations and transformations. The resulting matrix represents a new set of relations derived from the original matrices.
Tips
- Incorrect Dimensions: Ensure that the number of columns in Matrix A equals the number of rows in Matrix B.
- Mistakes in Arithmetic: Double-check calculations, especially when summing products, to avoid small errors leading to incorrect final answers.
AI-generated content may contain errors. Please verify critical information