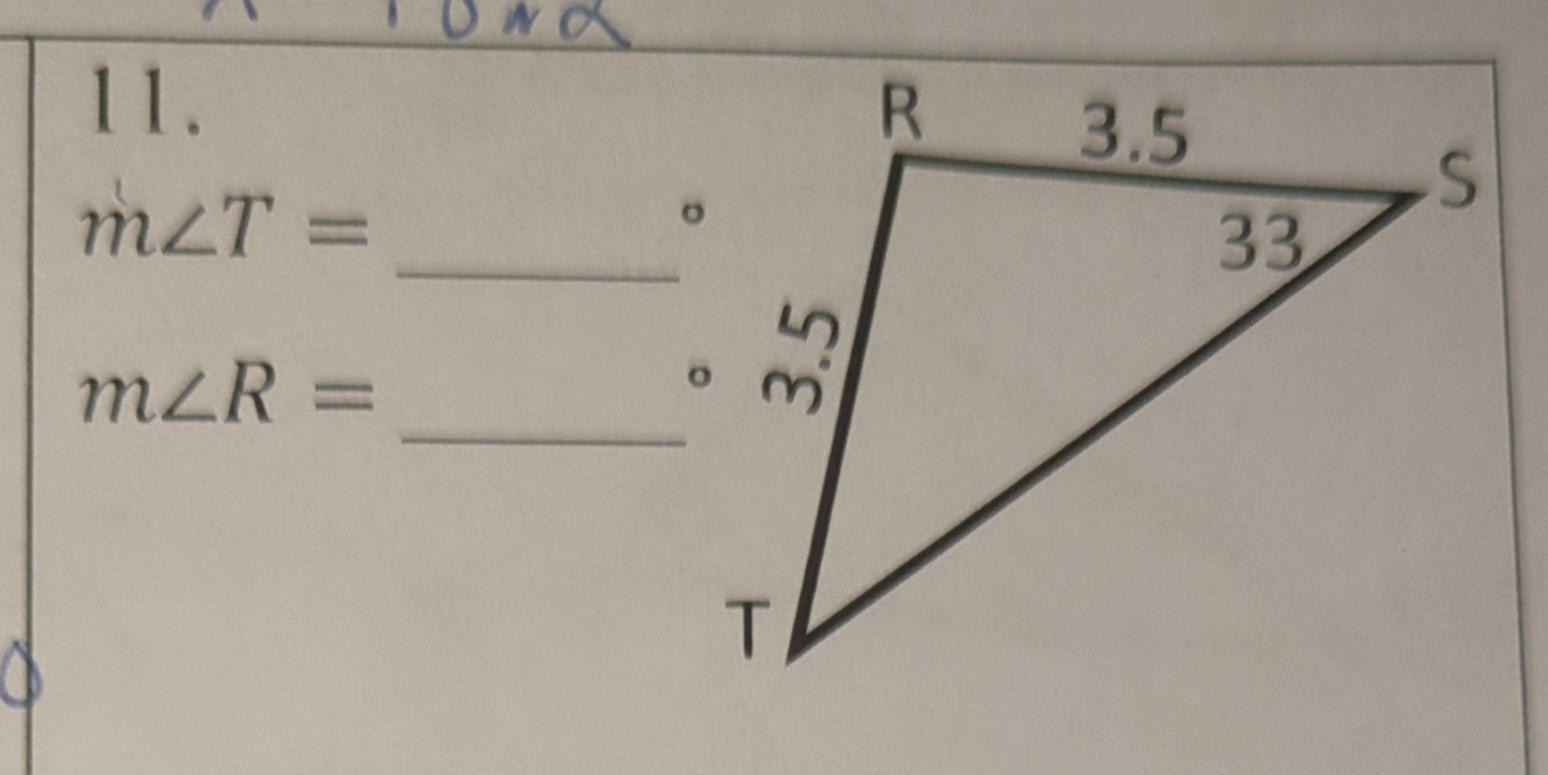
m∠T = _____°; m∠R = _____°
Understand the Problem
The question is asking for the measures of angles T and R in a triangle with given side lengths and an angle measurement. To find these measures, we may use the properties of triangles, such as the sum of angles in a triangle equaling 180 degrees.
Answer
m∠T = 114°; m∠R = 33°
Answer for screen readers
m∠T = 114°; m∠R = 33°
Steps to Solve
-
Identify Given Information The triangle has one known angle, ∠S = 33°, and the lengths of two sides, RT = 3.5 and RS = 3.5. We need to find the measures of angles T and R.
-
Use the Triangle Sum Theorem According to the Triangle Sum Theorem, the sum of the angles in a triangle is 180°: $$ m∠T + m∠R + m∠S = 180° $$
-
Substitute the Known Angle Substituting the value of ∠S into the equation: $$ m∠T + m∠R + 33° = 180° $$
-
Simplify the Equation Rearranging the equation gives: $$ m∠T + m∠R = 180° - 33° $$ $$ m∠T + m∠R = 147° $$
-
Finding Angles Using the Law of Sines Use the Law of Sines to relate the sides and angles: $$ \frac{RT}{\sin m∠S} = \frac{RS}{\sin m∠R} = \frac{TS}{\sin m∠T} $$
With RT = RS = 3.5, this leads to: $$ \frac{3.5}{\sin 33°} = \frac{3.5}{\sin m∠R} $$
-
Solve for Angle R Since the sides are equal: $$ \sin m∠R = \sin 33° $$ Thus, ( m∠R = 33° ).
-
Substitute to Find Angle T Now substitute this back into the simplified angle equation: $$ m∠T + 33° = 147° $$ Therefore: $$ m∠T = 147° - 33° $$ $$ m∠T = 114° $$
m∠T = 114°; m∠R = 33°
More Information
In triangle settings, when two sides are equal, angles opposite those sides are also equal. Here, finding one angle allowed for easy calculation of the other.
Tips
- Confusing Angles: Sometimes, it can be easy to mix the angles T and R, leading to incorrect assignments.
- Forgetting the Sum Rule: Not applying the Triangle Sum Theorem correctly can cause an oversight in angle calculations.
AI-generated content may contain errors. Please verify critical information