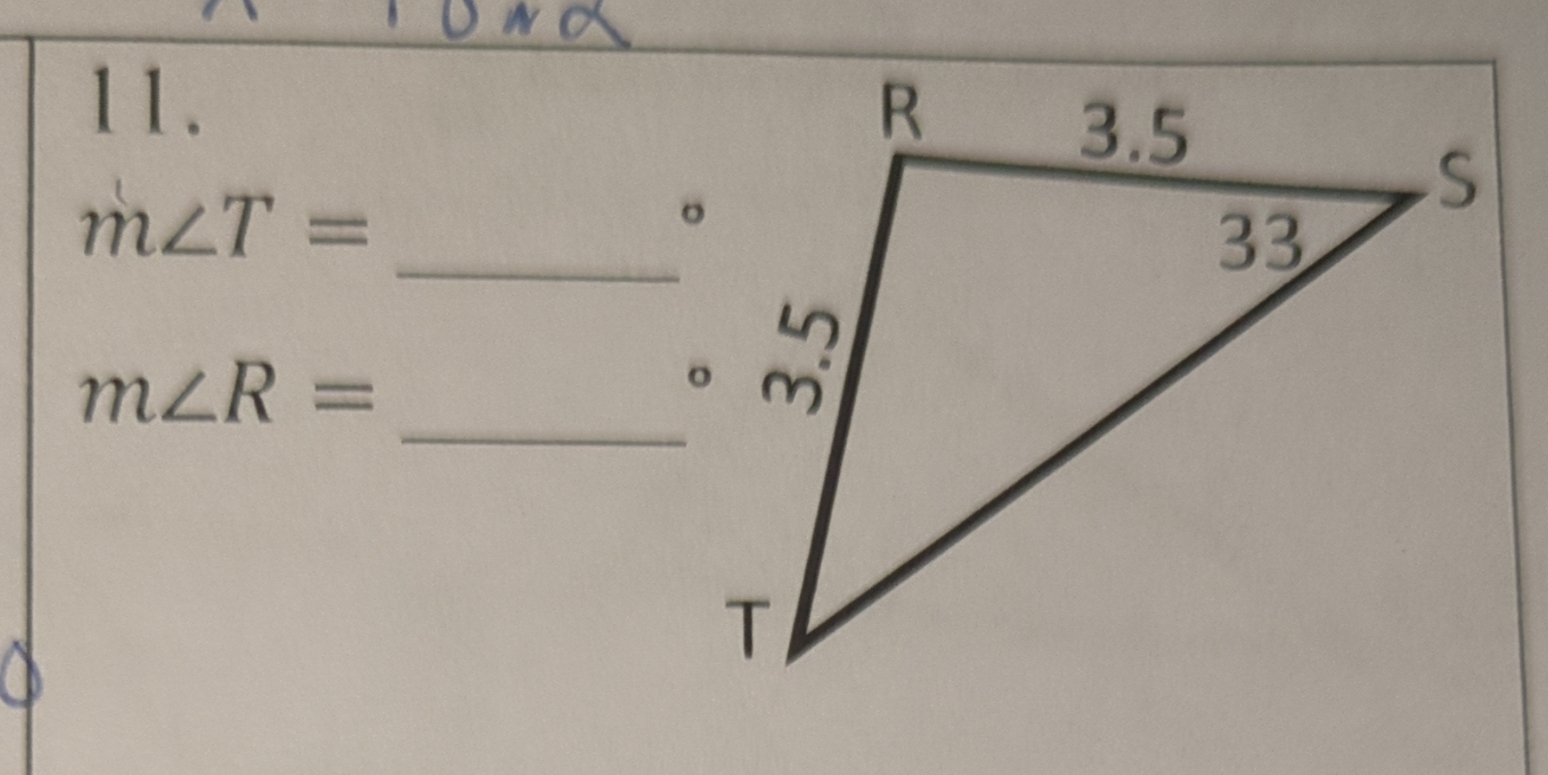
m∠T = _____° m∠R = _____°

Steps to Solve

1. Identify Given Values

We have the following information:

• Side $RS = 3.5$ units
• Angle $S = 33^\circ$
• Side $RT = 3.5$ units (since $RT$ is opposite to angle $S$)

2. Apply the Law of Sines

Using the Law of Sines, we can set up the equation:

$$ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} $$

For our triangle, this becomes:

$$ \frac{3.5}{\sin(33^\circ)} = \frac{3.5}{\sin(T)} $$

Since the sides are equal, we can simplify it to:

$$ \frac{1}{\sin(33^\circ)} = \frac{1}{\sin(T)} $$

3. Calculate Angle T

From the equation $\sin(T) = \sin(33^\circ)$:

Thus, we have: $$ T = 33^\circ $$

However, angle $T$ cannot equal $S$ because we have a triangle. Therefore, we calculate it using the known fact that the sum of angles in a triangle is $180^\circ$.

$$ T + R + S = 180^\circ $$

4. Substituting the Known Angles

Substituting $S = 33^\circ$ and $T = R$ due to symmetry:

$$ T + T + 33^\circ = 180^\circ $$

5. Solve for Angle T

Now simplify the equation:

$$ 2T + 33^\circ = 180^\circ $$

Subtract $33^\circ$ from both sides:

$$ 2T = 147^\circ $$

Now divide by 2:

$$ T = 73.5^\circ $$

Thus, $m∠T = 73.5^\circ$.

6. Find Angle R

Since triangle properties yield that $R = T$, we have:

$$ m∠R = 73.5^\circ $$