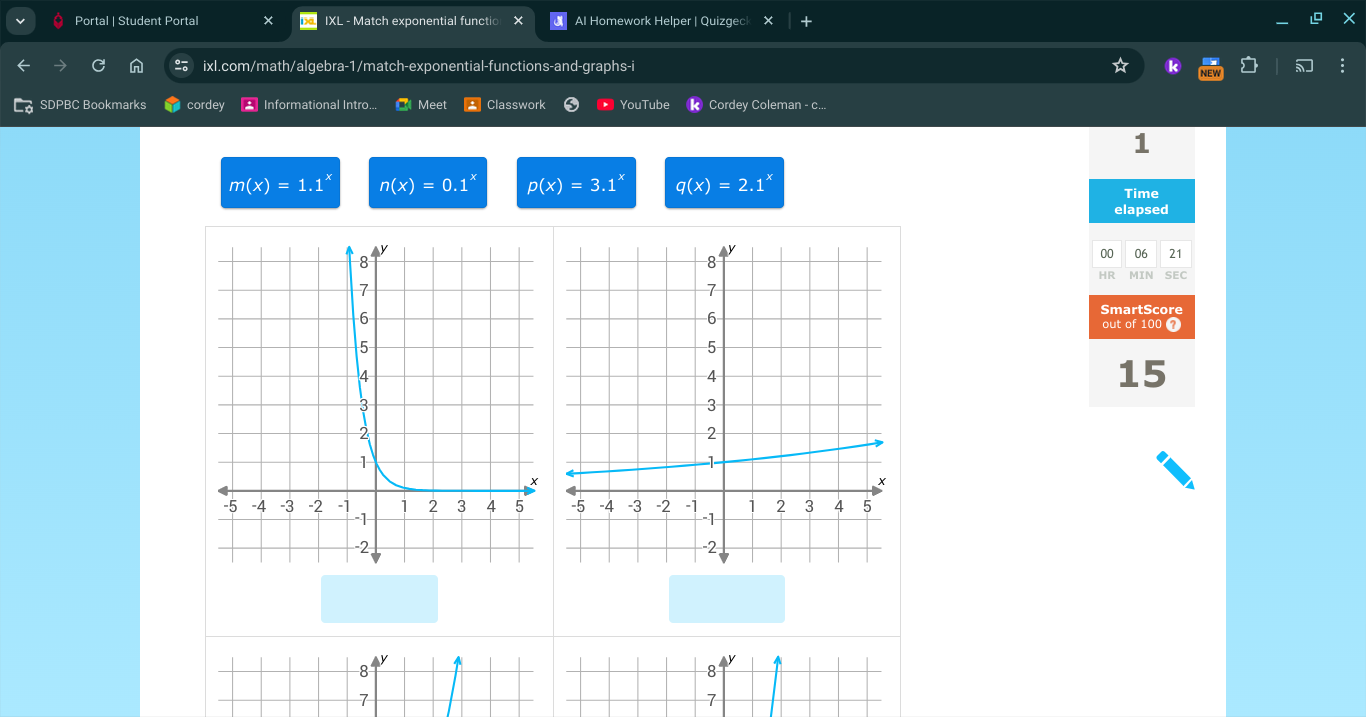
Match the exponential functions m(x) = 1.1^x, n(x) = 0.1^x, p(x) = 3.1^x, and q(x) = 2.1^x with their corresponding graphs.
Understand the Problem
The question is related to matching exponential functions with their corresponding graphs. It requires understanding the characteristics of different exponential functions represented in the image.
Answer
- $m(x)$ → gradual rise - $n(x)$ → sharp decline - $p(x)$ → steep rise - $q(x)$ → moderate rise
Answer for screen readers
- $m(x)$ matches with the gradual growth graph.
- $n(x)$ matches with the sharp decline graph.
- $p(x)$ matches with the steep growth graph.
- $q(x)$ matches with the moderate growth graph.
Steps to Solve
-
Identify the Characteristics of Each Function Observe the given functions:
- $m(x) = 1.1^x$
- $n(x) = 0.1^x$
- $p(x) = 3.1^x$
- $q(x) = 2.1^x$
Recognize the base of each function: greater than 1 indicates exponential growth, while between 0 and 1 indicates exponential decay.
-
Analyze the Graphs Look at each graph to understand their general trends:
- An exponential growth graph will rise steeply to the right and approach zero to the left.
- An exponential decay graph will fall steeply to the right and rise towards zero to the left.
-
Match Functions to Their Graphs Based on the characteristics:
- $m(x) = 1.1^x$ and $q(x) = 2.1^x$ are growth functions. The one that rises more steeply (larger base) is the one that matches $p(x)$.
- $n(x) = 0.1^x$ is a decay function and will match the graph that falls sharply.
-
Conclude Graph Matches Match each function:
- $m(x) = 1.1^x \to$ Graph that rises gradually
- $n(x) = 0.1^x \to$ Graph that falls sharply
- $p(x) = 3.1^x \to$ Graph that rises steeply
- $q(x) = 2.1^x \to$ Graph that also rises, but less steeply than $p(x)$
- $m(x)$ matches with the gradual growth graph.
- $n(x)$ matches with the sharp decline graph.
- $p(x)$ matches with the steep growth graph.
- $q(x)$ matches with the moderate growth graph.
More Information
Exponential functions are characterized by their base values. Bases greater than 1 produce growth, while bases less than 1 produce decay. The greater the base for growth, the steeper the graph rises.
Tips
- Confusing growth and decay functions by not paying attention to the base value.
- Not noting the steepness of growth, which can lead to incorrect matches.
AI-generated content may contain errors. Please verify critical information