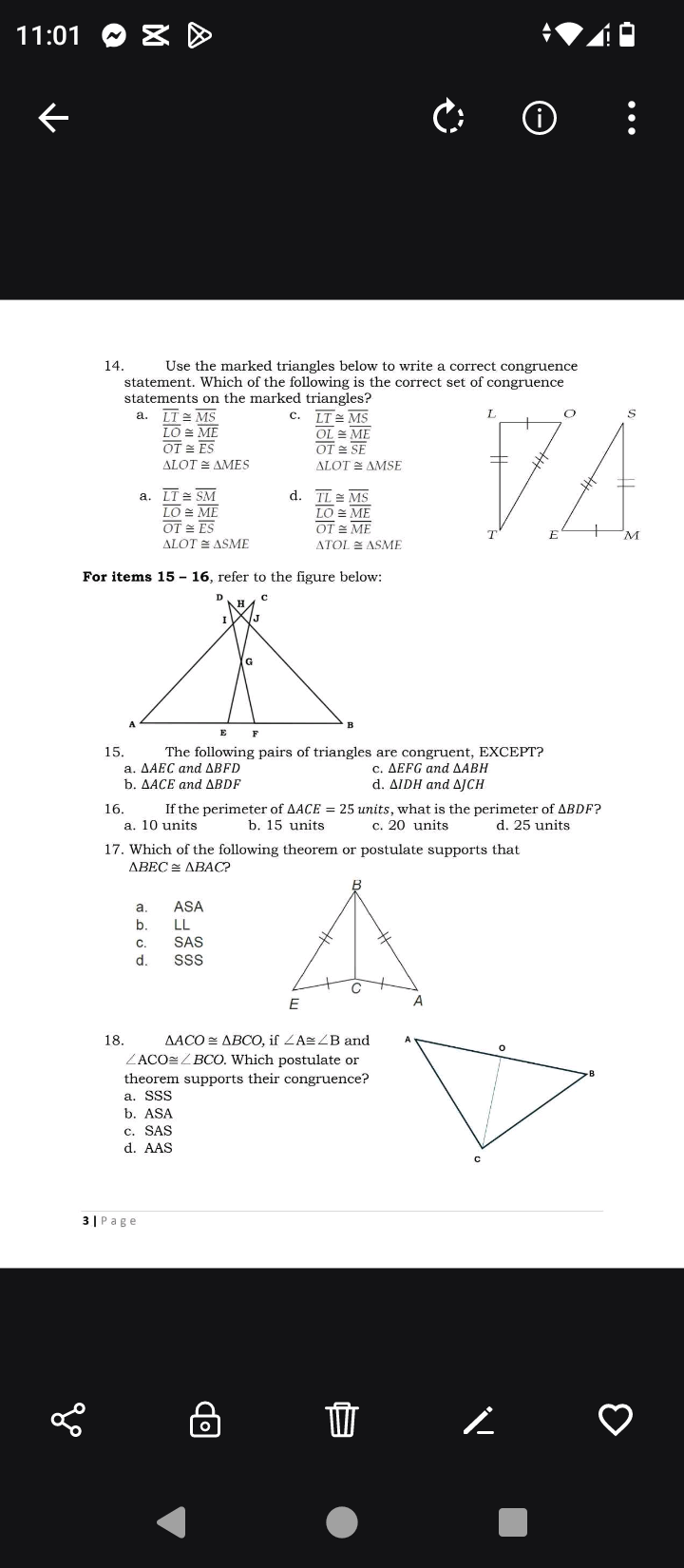
A variety of geometry questions related to congruent triangles.
Understand the Problem
The image contains multiple geometry questions related to triangle congruence and properties. It includes problems asking to identify correct congruence statements, determine which pairs of triangles are congruent, calculate perimeters, and identify theorems or postulates that support triangle congruence.
Answer
The correct congruence statement is option **c**: $\overline{LT} \cong \overline{MS}, \overline{OL} \cong \overline{ME}, \overline{OT} \cong \overline{SE}, \triangle LOT \cong \triangle MSE$.
Answer for screen readers
The correct congruence statement is option c: $\overline{LT} \cong \overline{MS}$, $\overline{OL} \cong \overline{ME}$, $\overline{OT} \cong \overline{SE}$, $\triangle LOT \cong \triangle MSE$.
Steps to Solve
-
Identify congruent segments and angles Review the marked triangles and determine which sides and angles correspond. In the options given, check each segment's notation to ensure congruency.
-
Write the congruence statements Based on the identified congruences, formulate the appropriate congruence statement. For example, if $\overline{LT} \cong \overline{MS}$, then the corresponding triangles would be $\triangle LOT \cong \triangle MES$.
-
Evaluate each option for correctness Check each option given (a, b, c, d) to validate that all stated congruences are accurate.
-
Select the correct answer Choose the option that contains all true congruence statements and correctly represents the triangle congruence.
The correct congruence statement is option c: $\overline{LT} \cong \overline{MS}$, $\overline{OL} \cong \overline{ME}$, $\overline{OT} \cong \overline{SE}$, $\triangle LOT \cong \triangle MSE$.
More Information
Congruence statements must correctly reflect the relationships between sides and angles of the triangles. Mislabeling segments or angles can lead to incorrect conclusions about triangle similarity or congruence.
Tips
- Misreading or mislabeling the sides and angles can lead to incorrect congruence statements.
- Overlooking the correct notation (such as using $\overline{SM}$ instead of $\overline{MS}$) can invalidate the statements.
AI-generated content may contain errors. Please verify critical information