M = 1 + 3 / 4 / (2 + 1 / (1 - 1 / 4)) Efecúe:
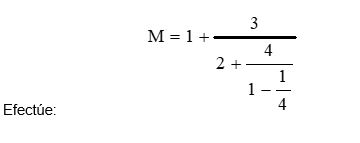
Understand the Problem
La pregunta está pidiendo resolver la ecuación dada para encontrar el valor de M. Esto implica simplificar la expresión y realizar las operaciones adecuadamente.
Answer
$M = \frac{49}{40}$
Answer for screen readers
El valor de $M$ es $\frac{49}{40}$.
Steps to Solve
- Resolver el denominador interno
Primero, resolvemos el denominador de la fracción interna: $1 - \frac{1}{4}$.
Calculamos: $$ 1 - \frac{1}{4} = \frac{4}{4} - \frac{1}{4} = \frac{3}{4} $$
- Sustituir el denominador en la expresión
Sustituimos el resultado en la expresión original de $M$: $$ M = 1 + \frac{3}{4} \div \left(2 + \frac{1}{\frac{3}{4}}\right) $$
- Calcular la fracción en el denominador
Ahora, calculamos la fracción: $\frac{1}{\frac{3}{4}}$, que se convierte en: $$ \frac{1}{\frac{3}{4}} = \frac{4}{3} $$
- Sustituir y simplificar la expresión
Ahora sustituimos esto de nuevo en $M$: $$ M = 1 + \frac{3}{4} \div \left(2 + \frac{4}{3}\right) $$
- Resolver la suma en el denominador
Calculamos la suma en el denominador: $$ 2 + \frac{4}{3} = \frac{6}{3} + \frac{4}{3} = \frac{10}{3} $$
- Realizar la división
Sustituimos eso en $M$ y resolvemos la división: $$ M = 1 + \frac{3}{4} \div \frac{10}{3} $$
Esto es equivalente a multiplicar por el recíproco: $$ = 1 + \frac{3}{4} \times \frac{3}{10} $$
- Multiplicar y simplificar
Calculamos el producto: $$ \frac{3 \times 3}{4 \times 10} = \frac{9}{40} $$
Entonces: $$ M = 1 + \frac{9}{40} $$
- Suma final
Convertimos $1$ a fracción con el mismo denominador: $$ M = \frac{40}{40} + \frac{9}{40} = \frac{49}{40} $$
El valor de $M$ es $\frac{49}{40}$.
More Information
El resultado $\frac{49}{40}$ también se puede expresar como un número mixto. Esto representa la suma de una parte entera y una parte fraccionaria.
Tips
- No simplificar adecuadamente al restar o sumar fracciones. Recuerda siempre encontrar un denominador común.
- Olvidar que dividir por una fracción equivale a multiplicar por su recíproco. Este es un paso común que se pasa por alto.
AI-generated content may contain errors. Please verify critical information