lim[z->-5] [(1 + 1/z)/ (z+5)]
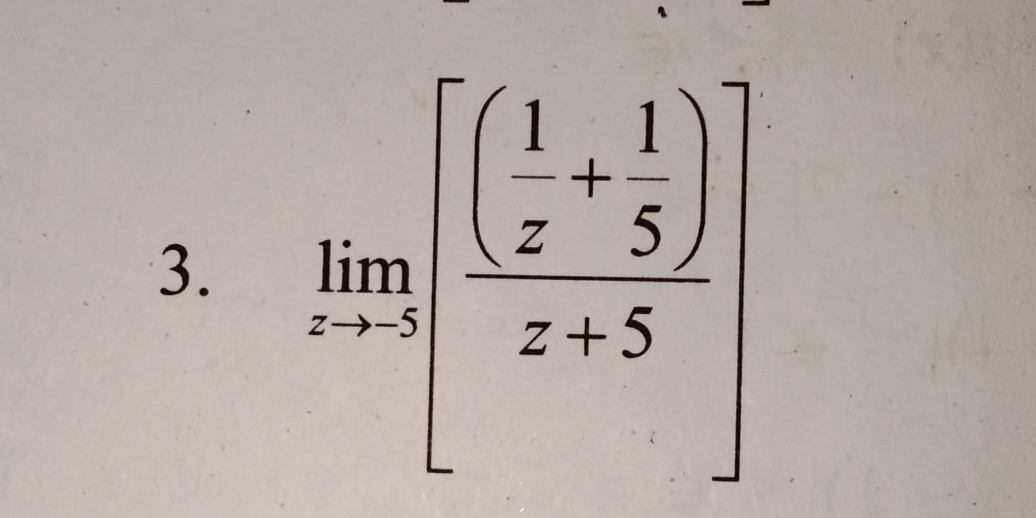
Understand the Problem
The question is asking to find the limit of the given expression as z approaches -5. This involves analyzing the function and determining what value it approaches without directly substituting z = -5, as that might lead to an indeterminate form.
Answer
The limit is $-\frac{1}{25}$.
Answer for screen readers
The limit is ( -\frac{1}{25} ).
Steps to Solve
-
Identify the Expression The limit is given as: $$ \lim_{z \to -5} \frac{1 + \frac{1}{z}}{z + 5} $$
-
Simplify the Expression Substitute the value of ( z ) approaching -5: $$ \frac{1 + \frac{1}{-5}}{-5 + 5} = \frac{1 - \frac{1}{5}}{0} $$ This leads to an indeterminate form ( \frac{0}{0} ).
-
Rearranging the Limit To resolve the indeterminate form, simplify the numerator: $$ 1 + \frac{1}{z} = \frac{z + 1}{z} $$
Thus, rewrite the limit: $$ \lim_{z \to -5} \frac{\frac{z + 1}{z}}{z + 5} $$
-
Combine the Expression Rewrite the limit using the simplified numerator: $$ \lim_{z \to -5} \frac{z + 1}{z(z + 5)} $$
-
Evaluate the Limit by Substitution Now substitute ( z = -5 ): $$ \frac{-5 + 1}{-5(-5 + 5)} = \frac{-4}{-5 \cdot 0} $$ This still leads to another indeterminate form.
-
Use L'Hôpital's Rule Since we're still facing ( \frac{0}{0} ), apply L'Hôpital's Rule (derivatives of the numerator and denominator): $$ \text{Numerator: } \frac{d}{dz}(1 + \frac{1}{z}) = -\frac{1}{z^2} $$
$$ \text{Denominator: } \frac{d}{dz}(z + 5) = 1 $$
Thus, applying the rule: $$ \lim_{z \to -5} -\frac{1}{z^2} $$
- Final Substitute to Find the Limit Substituting ( z = -5 ): $$ -\frac{1}{(-5)^2} = -\frac{1}{25} $$
The limit is ( -\frac{1}{25} ).
More Information
This limit demonstrates how to manage indeterminate forms by simplifying the expression and applying L'Hôpital's Rule when necessary. Understanding when to use derivatives is crucial in calculus.
Tips
- Failing to simplify the expression first, leading to confusion when directly substituting ( z = -5 ).
- Not recognizing that the limit results in an indeterminate form, where L'Hôpital's rule should be applied.
AI-generated content may contain errors. Please verify critical information