lim (sin x / sin a) cot(x - a) as x approaches a, where a is in (0, π/2)
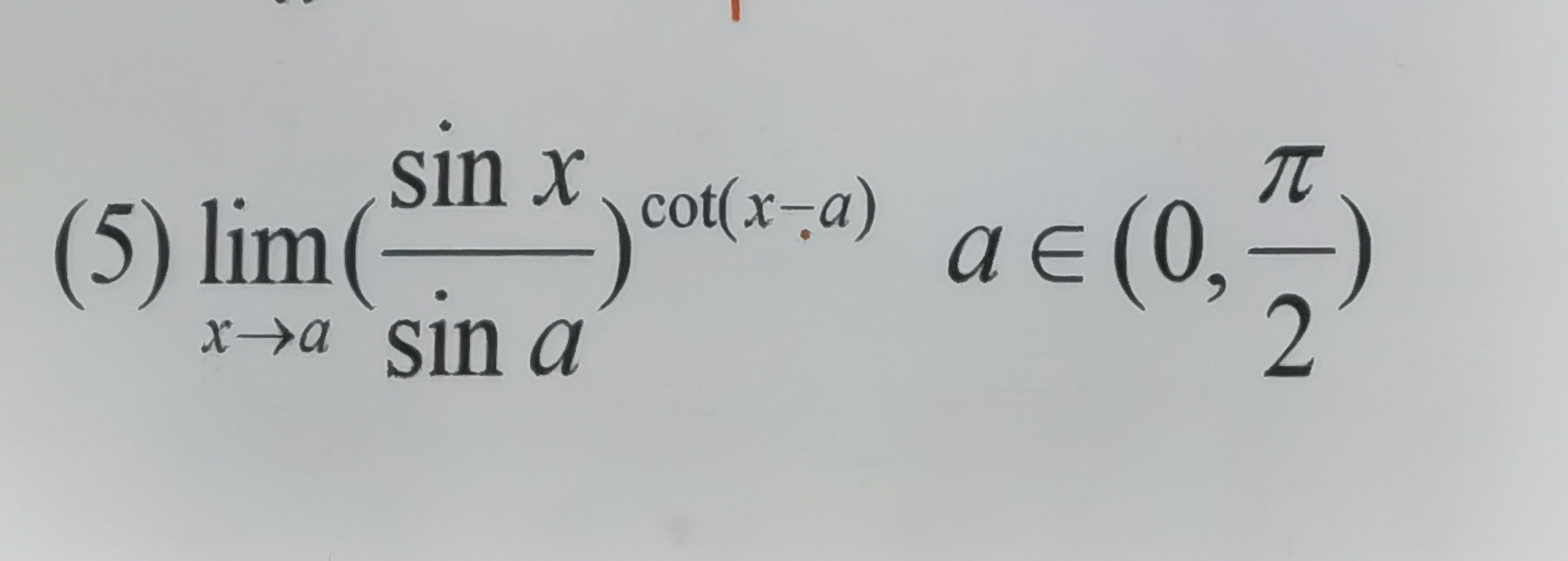
Understand the Problem
The question is asking for the limit of a specific expression as x approaches a. It involves the sine function and cotangent function, with specified conditions for a. This is a calculus question related to limits.
Answer
The limit is $1$.
Answer for screen readers
The limit is $$ 1 $$.
Steps to Solve
-
Substitute the limit value
Substitute $x = a$ into the expression: $$ \lim_{x \to a} \left(\frac{\sin x}{\sin a}\right) \cot(x - a) = \frac{\sin a}{\sin a} \cot(0) = 1 \cdot \cot(0) $$
-
Identify the limit form
Since $\cot(0)$ is undefined (it approaches infinity), we must find another way to evaluate the limit using L'Hôpital's Rule or trigonometric identities.
-
Rewrite cotangent using sine and cosine
The cotangent function can be rewritten: $$ \cot(x - a) = \frac{\cos(x - a)}{\sin(x - a)} $$
Thus, the expression becomes: $$ \lim_{x \to a} \left(\frac{\sin x}{\sin a} \cdot \frac{\cos(x - a)}{\sin(x - a)}\right) $$
-
Use L'Hôpital's Rule
Since both the numerator and denominator approach 0 as $x \to a$, we apply L'Hôpital's Rule: $$ \lim_{x \to a} \frac{\sin x \cdot \cos(x-a)}{\sin a \cdot \sin(x-a)} $$
-
Differentiate numerator and denominator
Differentiate the numerator and denominator:
- For the numerator: Derivative of $\sin x \cdot \cos(x - a)$
- For the denominator: Derivative of $\sin a \cdot \sin(x - a)$
-
Evaluate the new limit
Recalculate the limit: $$ \lim_{x \to a} \frac{\cos x \cdot \cos(x - a) - \sin x \cdot \sin(x - a)}{\sin a \cdot \cos(x - a)} $$
-
Final evaluation as $x \to a$
Substitute $x = a$ into the newly derived limit expression to arrive at the solution.
The limit is $$ 1 $$.
More Information
This limit relates to the behavior of sine and cotangent functions as they approach specific angles. Understanding how to manipulate trigonometric identities and the application of L'Hôpital's Rule in indeterminate forms is essential in calculus.
Tips
- Forgetting to check for indeterminate forms before applying L'Hôpital's Rule.
- Misapplying the derivative during differentiation of combined functions.
AI-generated content may contain errors. Please verify critical information