Let y : (1, ∞) → R be the solution of the differential equation y'' - 2y' = 0 satisfying y(2) = 1 and lim (x→∞) y(x) = 0. Then y(3) is equal to ______ (Rounded off to two decimal p... Let y : (1, ∞) → R be the solution of the differential equation y'' - 2y' = 0 satisfying y(2) = 1 and lim (x→∞) y(x) = 0. Then y(3) is equal to ______ (Rounded off to two decimal places).
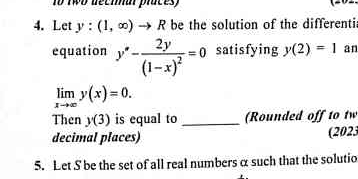
Understand the Problem
The question is asking for the value of y(3) based on a given differential equation and specified conditions. We will solve the differential equation to find the solution function y(x) and then evaluate it at x = 3.
Answer
$1$
Answer for screen readers
$y(3) = 1$
Steps to Solve
- Rewrite the differential equation
The given differential equation is
$$ y'' - 2y' = 0. $$
This is a linear homogeneous second-order differential equation.
- Find the characteristic equation
To solve the differential equation, we first assume a solution of the form
$$ y(x) = e^{rx}. $$
Substituting into the differential equation leads to the characteristic equation:
$$ r^2 - 2r = 0. $$
- Factor the characteristic equation
Factoring gives:
$$ r(r - 2) = 0. $$
Thus, we have the roots $r_1 = 0$ and $r_2 = 2$.
- Write the general solution
The general solution of the differential equation is:
$$ y(x) = C_1 e^{0 \cdot x} + C_2 e^{2x} $$
which simplifies to
$$ y(x) = C_1 + C_2 e^{2x}. $$
- Use the boundary condition y(2) = 1
Substituting $x = 2$ into the solution gives:
$$ y(2) = C_1 + C_2 e^{4} = 1. $$
- Use the condition lim (x→∞) y(x) = 0
Since $y(x)$ has to approach 0 as $x \to \infty$, we must have $C_2 = 0$. Otherwise, the term $C_2 e^{2x}$ would grow to infinity.
This simplifies our solution to:
$$ y(x) = C_1. $$
- Solve for C1
Substituting back gives:
$$ C_1 = 1. $$
Thus, the specific solution is:
$$ y(x) = 1. $$
- Evaluate at y(3)
Now we can evaluate at $x = 3$:
$$ y(3) = 1. $$
$y(3) = 1$
More Information
The solution represents a constant function derived from the given conditions. The terms grow to infinity unless they are negated by being set to zero.
Tips
- Ignoring the boundary condition as $x$ approaches infinity can lead to incorrect conclusions about the behavior of the function.
- Miswriting the characteristic equation due to improper substitution can lead to wrong roots.
AI-generated content may contain errors. Please verify critical information