Let h(x) = P(x) / (2(x+5)(2x+1)). What is the domain of definition of h(x)? Simplify h(x), and calculate h(-2). Solve h(x) = 3.
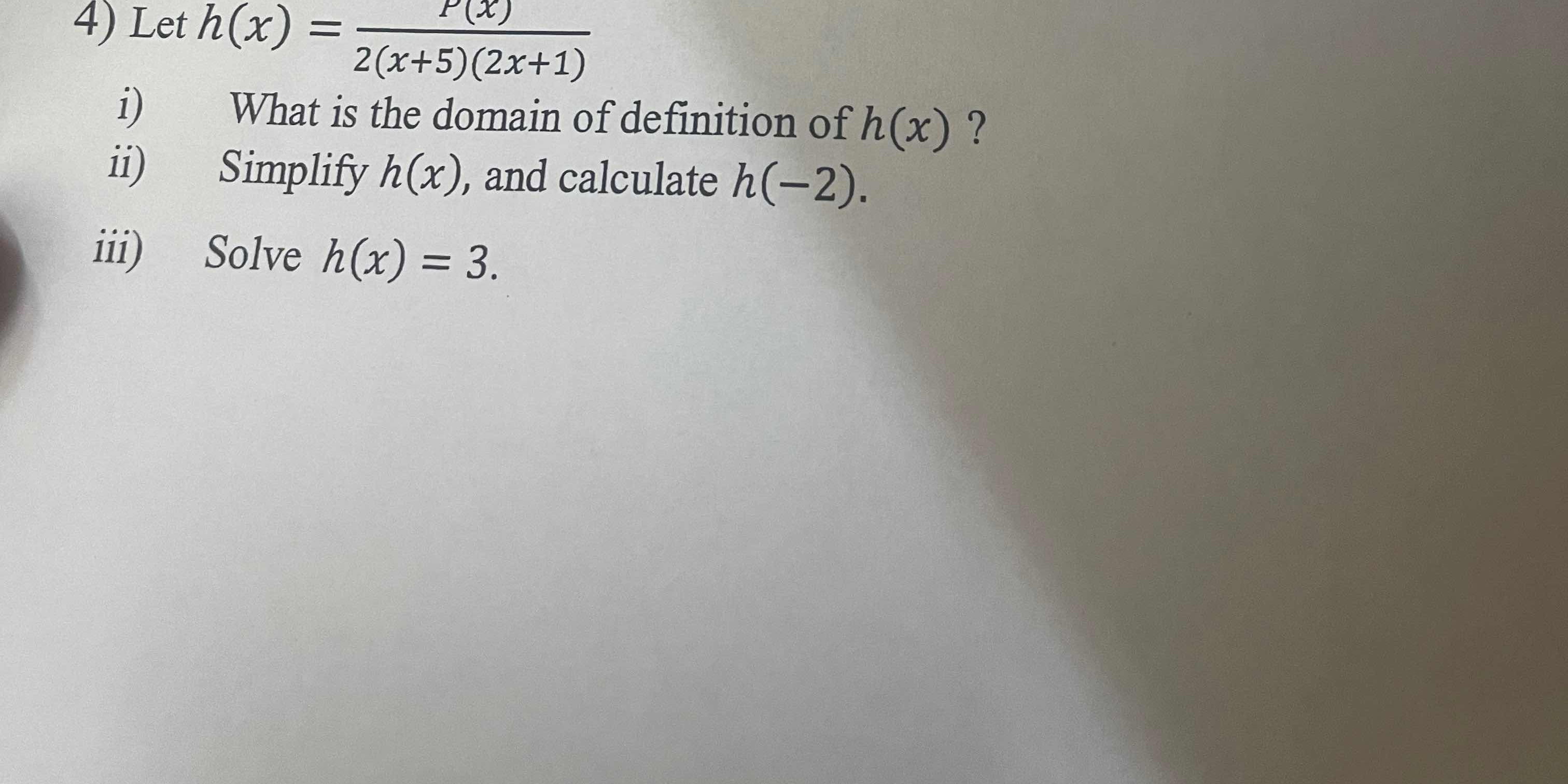
Understand the Problem
The question is asking to analyze the function h(x), including finding the domain of definition, simplifying the function and calculating its value at a specific point, and solving an equation involving the function. This involves understanding rational functions and their properties.
Answer
Domain: $x \in \mathbb{R}, x \neq -5, x \neq -\frac{1}{2}$; $h(-2) = \frac{P(-2)}{-18}$; $h(x) = 3 \implies P(x) = 6(x + 5)(2x + 1)$.
Answer for screen readers
The domain of definition of $h(x)$ is all real numbers except $x = -5$ and $x = -\frac{1}{2}$.
To calculate $h(-2)$, $$ h(-2) = \frac{P(-2)}{-18} $$.
The equation $h(x) = 3$ leads to $$ P(x) = 6(x + 5)(2x + 1). $$
Steps to Solve
- Finding the Domain of Definition
To find the domain, identify where the denominator is zero since these values make the function undefined. Set the denominator equal to zero: $$ 2(x + 5)(2x + 1) = 0 $$ This equation is satisfied when either $(x + 5) = 0$ or $(2x + 1) = 0$.
Solving for $x$ gives:
- From $x + 5 = 0$: $$ x = -5 $$
- From $2x + 1 = 0$: $$ 2x = -1 \Rightarrow x = -\frac{1}{2} $$
Thus, the domain is all real numbers except $x = -5$ and $x = -\frac{1}{2}$.
- Simplifying h(x)
The function $h(x)$ can be expressed as: $$ h(x) = \frac{P(x)}{2(x + 5)(2x + 1)} $$
Assuming $P(x)$ does not introduce any additional restrictions, $h(x)$ is written as is since we need more information on $P(x)$ to simplify further.
- Calculating h(-2)
Now substitute $x = -2$ into the function: $$ h(-2) = \frac{P(-2)}{2(-2 + 5)(2(-2) + 1)} $$ Calculate the denominator: $$ 2(-2 + 5) = 2(3) = 6 $$ $$ 2(-2) + 1 = -4 + 1 = -3 $$
Thus, $$ h(-2) = \frac{P(-2)}{6 \cdot (-3)} = \frac{P(-2)}{-18} $$
- Solving h(x) = 3
Set the function equal to 3: $$ \frac{P(x)}{2(x + 5)(2x + 1)} = 3 $$
Cross-multiply to remove the fraction: $$ P(x) = 3 \cdot 2(x + 5)(2x + 1) $$ Thus, $$ P(x) = 6(x + 5)(2x + 1) $$
You would then solve for $x$ once you have $P(x)$, based on further context or given specifics about the polynomial $P(x)$.
The domain of definition of $h(x)$ is all real numbers except $x = -5$ and $x = -\frac{1}{2}$.
To calculate $h(-2)$, $$ h(-2) = \frac{P(-2)}{-18} $$.
The equation $h(x) = 3$ leads to $$ P(x) = 6(x + 5)(2x + 1). $$
More Information
The domain indicates where the function is valid (avoids division by zero). Calculating $h(-2)$ reveals the function's output at that specific input. Solving $h(x) = 3$ shows how to express a polynomial in terms of a known function structure.
Tips
- Forgetting to exclude values that make the denominator zero in the domain.
- Misleading simplifications without specific knowledge of $P(x)$.
- Not carefully rearranging equations when cross-multiplying.
AI-generated content may contain errors. Please verify critical information