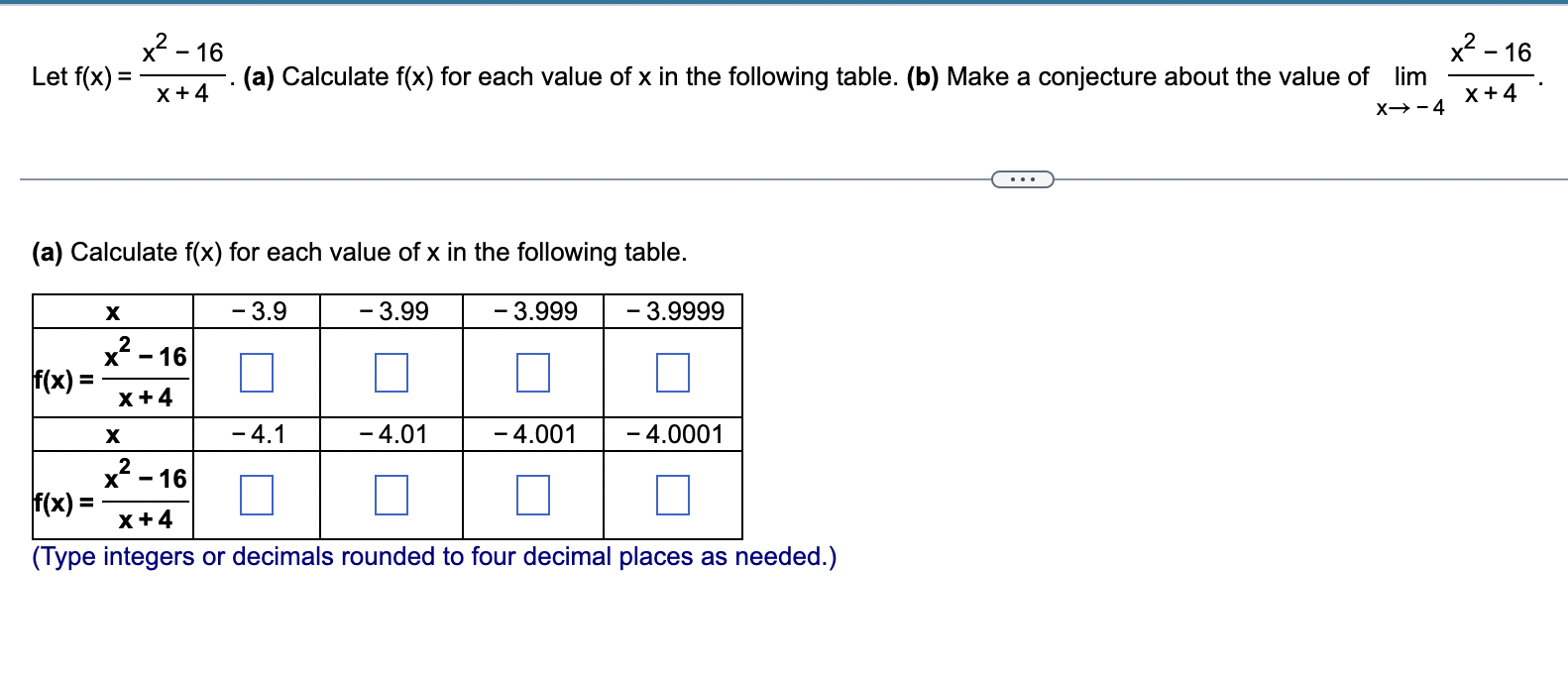
Let f(x) = (x² - 16) / (x + 4). (a) Calculate f(x) for each value of x in the following table. (b) Make a conjecture about the value of lim (x→-4) (x² - 16) / (x + 4).

Steps to Solve

1. Substitute values into the function
   Begin by substituting each value of ( x ) into the function ( f(x) = \frac{x^2 - 16}{x + 4} ).

2. Calculate ( f(-3.9) )
   Use ( x = -3.9 ):
   $$ f(-3.9) = \frac{(-3.9)^2 - 16}{-3.9 + 4} = \frac{15.21 - 16}{0.1} = \frac{-0.79}{0.1} = -7.9 $$

3. Calculate ( f(-3.99) )
   Use ( x = -3.99 ):
   $$ f(-3.99) = \frac{(-3.99)^2 - 16}{-3.99 + 4} = \frac{15.9201 - 16}{0.01} = \frac{-0.0799}{0.01} = -7.99 $$

4. Calculate ( f(-3.999) )
   Use ( x = -3.999 ):
   $$ f(-3.999) = \frac{(-3.999)^2 - 16}{-3.999 + 4} = \frac{15.992001 - 16}{0.001} = \frac{-0.007999}{0.001} = -7.999 $$

5. Calculate ( f(-3.9999) )
   Use ( x = -3.9999 ):
   $$ f(-3.9999) = \frac{(-3.9999)^2 - 16}{-3.9999 + 4} = \frac{15.99960001 - 16}{0.0001} = \frac{-0.00039999}{0.0001} = -7.9999 $$

6. Calculate ( f(-4.1) )
   Use ( x = -4.1 ):
   $$ f(-4.1) = \frac{(-4.1)^2 - 16}{-4.1 + 4} = \frac{16.81 - 16}{-0.1} = \frac{0.81}{-0.1} = -8.1 $$

7. Calculate ( f(-4.01) )
   Use ( x = -4.01 ):
   $$ f(-4.01) = \frac{(-4.01)^2 - 16}{-4.01 + 4} = \frac{16.0801 - 16}{-0.01} = \frac{0.0801}{-0.01} = -8.01 $$

8. Calculate ( f(-4.001) )
   Use ( x = -4.001 ):
   $$ f(-4.001) = \frac{(-4.001)^2 - 16}{-4.001 + 4} = \frac{16.008001 - 16}{-0.001} = \frac{0.008001}{-0.001} = -8.001 $$

9. Calculate ( f(-4.0001) )
   Use ( x = -4.0001 ):
   $$ f(-4.0001) = \frac{(-4.0001)^2 - 16}{-4.0001 + 4} = \frac{16.00040001 - 16}{-0.0001} = \frac{0.00040001}{-0.0001} = -8.0001 $$

10. Make a conjecture about the limit as ( x ) approaches -4
    As ( x ) approaches -4 from both sides, ( f(x) ) approaches -8. Thus, we can conjecture that: $$ \lim_{x \to -4} f(x) = -8 $$