Let D be the region enclosed by the surfaces z = 5 - x^2 - y^2 and z = 4x^2 + 4y^2. Set up the integrals that gives the volume of D in the order of integration dz dr dθ.
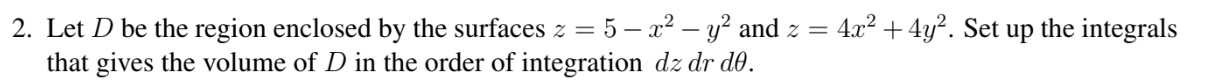
Understand the Problem
The question is asking to set up the integrals for the volume of a region D enclosed by two surfaces, given a specific order of integration. This involves determining the bounds for z, r, and θ based on the surfaces described.
Answer
The integral for the volume is \( V = \int_0^{2\pi} \int_0^1 \int_{4r^2}^{5 - r^2} r \, dz \, dr \, d\theta \).
Answer for screen readers
The integral setup for the volume ( V ) of the region ( D ) in the order ( dz , dr , d\theta ) is:
$$ V = \int_0^{2\pi} \int_0^1 \int_{4r^2}^{5 - r^2} r , dz , dr , d\theta $$
Steps to Solve
-
Identify the surfaces and their intersection
To find the volume enclosed by the two surfaces, we set them equal to find their intersection:
$$ 5 - x^2 - y^2 = 4x^2 + 4y^2 $$
This can be rearranged to:
$$ 5 = 5x^2 + 5y^2 $$
Dividing by 5 gives:
$$ 1 = x^2 + y^2 $$
This shows that the curves intersect at a circle of radius 1. -
Convert to polar coordinates
Using polar coordinates, where ( x = r \cos \theta ) and ( y = r \sin \theta ), the equation from the intersection becomes:
$$ r^2 = 1 $$
Thus, ( r ) ranges from 0 to 1 and ( \theta ) ranges from 0 to ( 2\pi ). -
Determine bounds for ( z )
From the surfaces defined:
- For the upper surface: ( z = 5 - r^2 )
- For the lower surface: ( z = 4r^2 )
The bounds for ( z ) go from the lower surface to the upper surface, which can be written as:
$$ z \text{ ranges from } 4r^2 \text{ to } 5 - r^2 $$
-
Set up the volume integral
The volume ( V ) can be expressed in polar coordinates as follows:
$$ V = \int_0^{2\pi} \int_0^1 \int_{4r^2}^{5 - r^2} r , dz , dr , d\theta $$
The ( r ) in the integrand accounts for the Jacobian when switching to polar coordinates.
The integral setup for the volume ( V ) of the region ( D ) in the order ( dz , dr , d\theta ) is:
$$ V = \int_0^{2\pi} \int_0^1 \int_{4r^2}^{5 - r^2} r , dz , dr , d\theta $$
More Information
This integral calculates the volume of the region D enclosed between the two surfaces. By integrating ( z ) first, we account for the vertical height at each horizontal radius ( r ) and angle ( \theta ).
Tips
- Forgetting to convert to polar coordinates may lead to incorrect bounds and integrals.
- Misidentifying which surface is upper and lower could lead to incorrect limits for ( z ). Always check the conditions of the surfaces at the intersection points.
AI-generated content may contain errors. Please verify critical information