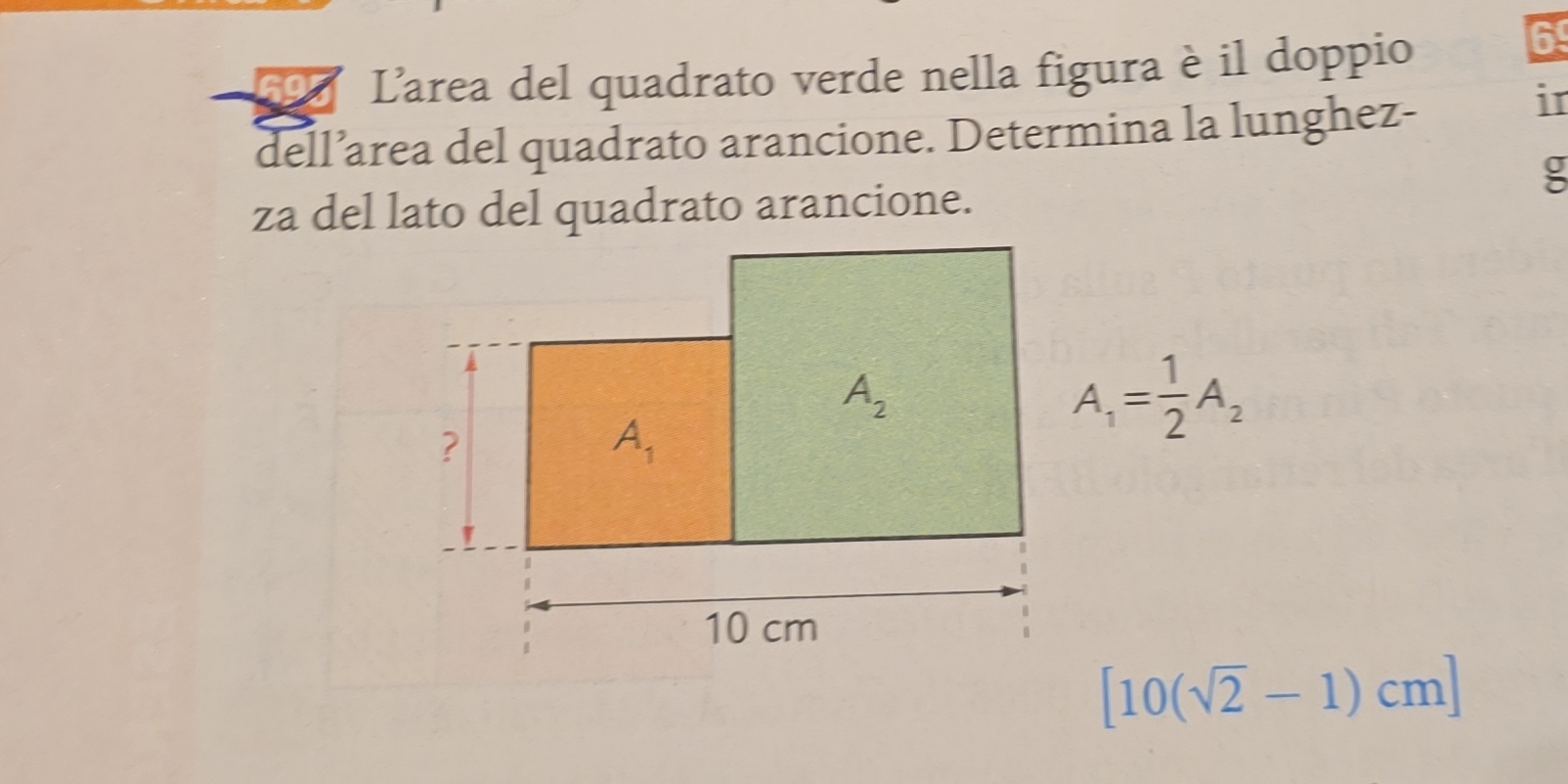
L'area del quadrato verde nella figura è il doppio dell'area del quadrato arancione. Determina la lunghezza del lato del quadrato arancione.

Steps to Solve

1. Identificare le aree dei quadrati Sia $A_1$ l'area del quadrato arancione e $A_2$ l'area del quadrato verde. Sappiamo che $A_2 = 2A_1$.

2. Espressione dell'area del quadrato arancione Se chiamiamo $l$ la lunghezza del lato del quadrato arancione, possiamo esprimere l'area come: $$ A_1 = l^2 $$

3. Espressione dell'area del quadrato verde Utilizzando la relazione tra le aree, possiamo scrivere: $$ A_2 = 2A_1 = 2l^2 $$

4. Stabilire la relazione con il quadrato verde Sappiamo che la lunghezza del lato del quadrato verde è: $$ L = 10 - l $$

5. Calcolare l'area del quadrato verde L'area del quadrato verde quindi è: $$ A_2 = (10 - l)^2 $$

6. Impostare l'equazione Impostiamo l'equazione tra le aree: $$ 2l^2 = (10 - l)^2 $$

7. Espandere e risolvere l'equazione Espandiamo il lato destro: $$ 2l^2 = 100 - 20l + l^2 $$

8. Riorganizzare l'equazione Portiamo tutto a sinistra per ottenere l'equazione quadratica: $$ 2l^2 - l^2 + 20l - 100 = 0 $$ $$ l^2 + 20l - 100 = 0 $$

9. Utilizzare la formula quadratica Applicando la formula quadratica $l = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, con $a = 1$, $b = 20$, e $c = -100$: $$ l = \frac{-20 \pm \sqrt{20^2 - 4 \cdot 1 \cdot (-100)}}{2 \cdot 1} $$

10. Calcolare la lunghezza del lato Calcoliamo il discriminante: $$ 20^2 + 400 = 800 $$ Quindi $$ l = \frac{-20 \pm \sqrt{800}}{2} = \frac{-20 \pm 20\sqrt{2}}{2} $$ Semplificando otteniamo: $$ l = -10 \pm 10\sqrt{2} $$ Poiché il lato non può essere negativo, prendiamo $l = 10(\sqrt{2} - 1)$.