Jack goes bowling. He has $35 to spend. He spends $6.25 to rent shoes. He spends $3.50 for each game he bowls. Which inequality can Jack use to determine g, the greatest number of... Jack goes bowling. He has $35 to spend. He spends $6.25 to rent shoes. He spends $3.50 for each game he bowls. Which inequality can Jack use to determine g, the greatest number of games he can bowl?
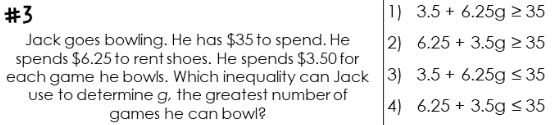
Understand the Problem
The question is asking to identify the correct inequality that Jack can use to determine the maximum number of bowling games he can afford, given his spending constraints.
Answer
The correct inequality is $6.25 + 3.5g \leq 35$.
Answer for screen readers
The correct inequality is $$ 6.25 + 3.5g \leq 35 $$.
Steps to Solve
-
Identify Fixed Costs Jack has a fixed cost of $6.25 for shoe rental. This must be subtracted from his total budget of $35.
-
Set Up the Cost Equation Let $g$ be the number of games Jack bowls. The cost for each game is $3.50. Thus, the total cost for bowling is $3.50g$.
-
Formulate the Total Cost Inequality The total costs (shoe rental + bowling games) must not exceed Jack's budget. Therefore, the inequality can be formulated as: $$ 6.25 + 3.5g \leq 35 $$
-
Subtract Fixed Costs from Budget Rearrange the inequality to isolate the variable term: $$ 3.5g \leq 35 - 6.25 $$
-
Calculate Remaining Budget Calculate the right side: $$ 35 - 6.25 = 28.75 $$ Thus, the inequality simplifies to: $$ 3.5g \leq 28.75 $$
The correct inequality is $$ 6.25 + 3.5g \leq 35 $$.
More Information
This inequality indicates the maximum number of games Jack can afford to bowl after accounting for the fixed cost of shoe rental. The calculation ensures that his total spending does not exceed his budget of $35.
Tips
- Ignoring Fixed Costs: Sometimes, students forget to include fixed costs like shoe rentals.
- Confusing Inequalities: Ensure you use the correct inequality symbol (≤ instead of ≥) to properly represent the spending limit.
AI-generated content may contain errors. Please verify critical information