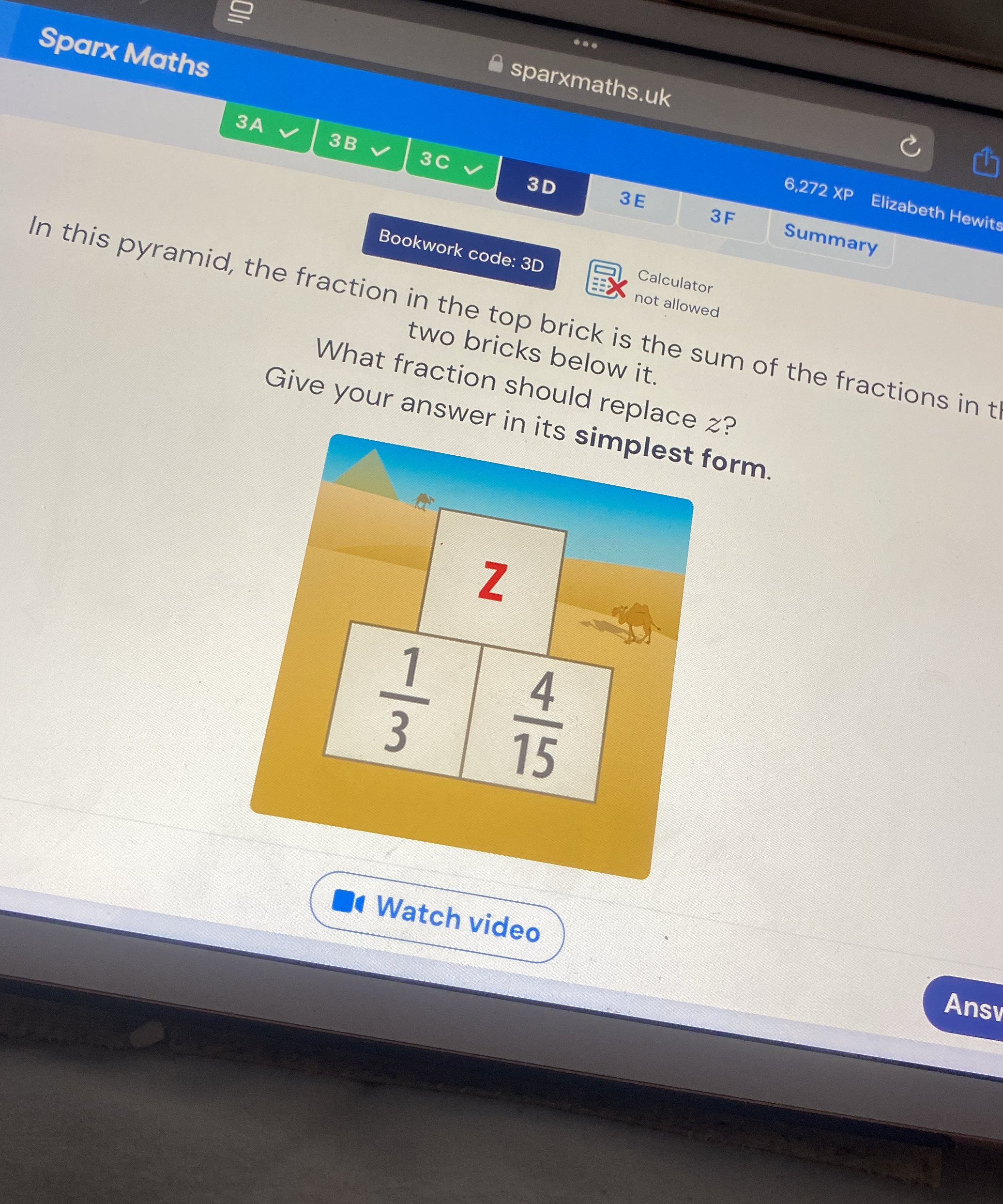
In this pyramid, the fraction in the top brick is the sum of the fractions in the two bricks below it. What fraction should replace z? Give your answer in its simplest form.
Understand the Problem
The question is asking to determine the value of the fraction 'z' in a pyramid structure where the fraction in the top brick is the sum of the fractions in the two bricks below it. The user needs to find 'z' given that the fractions below it are 1/3 and 4/15.
Answer
The fraction that should replace \( z \) is \( \frac{3}{5} \).
Answer for screen readers
The fraction that should replace ( z ) is ( \frac{3}{5} ).
Steps to Solve
- Find a common denominator
To add the fractions $\frac{1}{3}$ and $\frac{4}{15}$, we first need to find a common denominator. The least common multiple of 3 and 15 is 15.
- Convert fractions to have a common denominator
Convert $\frac{1}{3}$ so that it has the denominator of 15: $$ \frac{1}{3} = \frac{1 \times 5}{3 \times 5} = \frac{5}{15} $$ Now we have: $$ \frac{5}{15} \text{ and } \frac{4}{15} $$
- Add the fractions
Now we can add the two fractions: $$ z = \frac{5}{15} + \frac{4}{15} = \frac{5 + 4}{15} = \frac{9}{15} $$
- Simplify the fraction
Simplifying $\frac{9}{15}$ gives us: $$ z = \frac{9 \div 3}{15 \div 3} = \frac{3}{5} $$
The fraction that should replace ( z ) is ( \frac{3}{5} ).
More Information
The pyramid structure of fractions is a useful way to visualize how fractions can be combined. Adding fractions is essential in many areas of math and helps build understanding for more complex operations.
Tips
- Not finding a common denominator before adding.
- Forgetting to simplify the final fraction.
- Miscalculating addition when working with fractions.
AI-generated content may contain errors. Please verify critical information