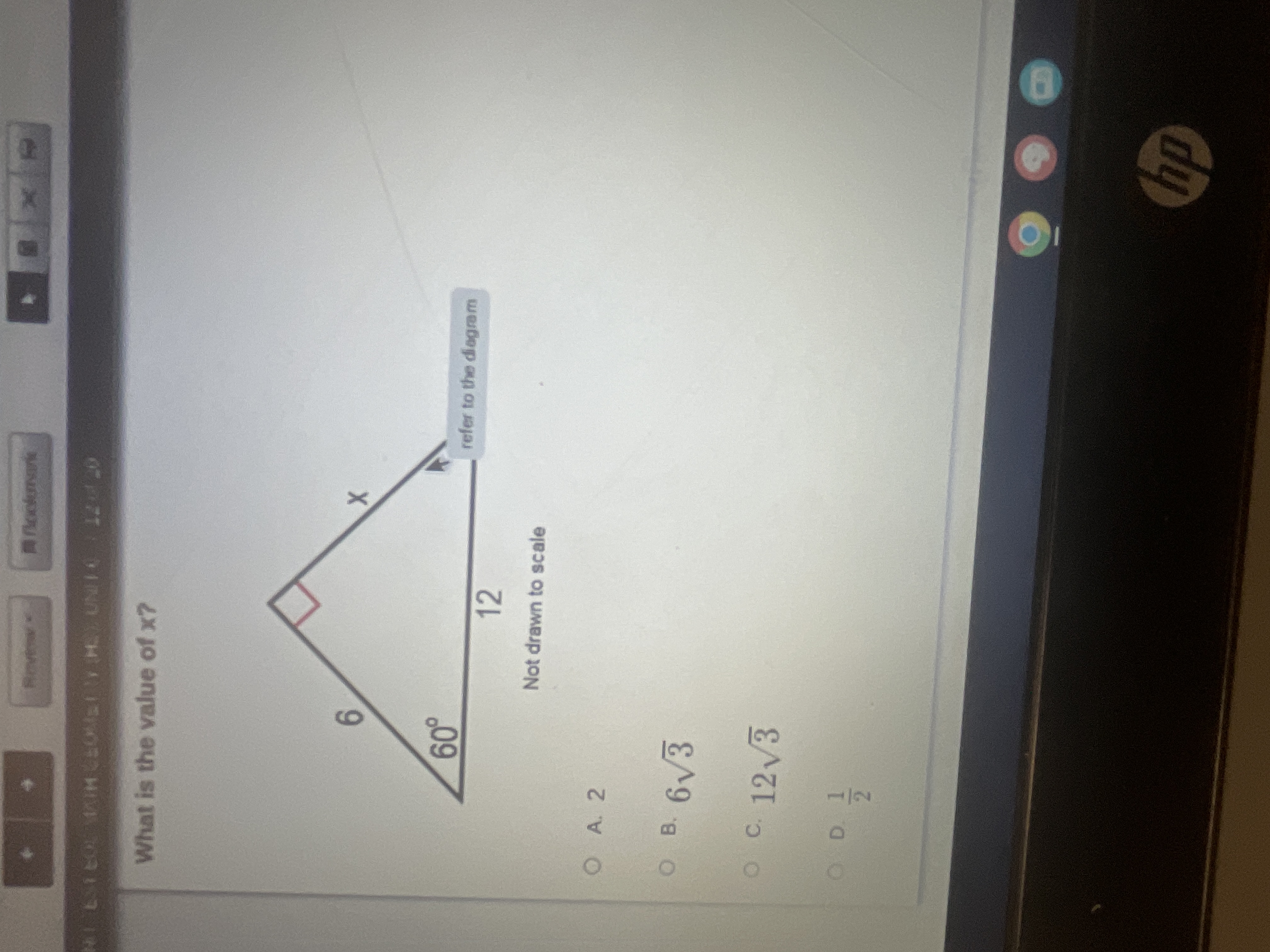
What is the value of x?

Steps to Solve

1. Identify the Given Information

We are given one angle of the triangle ($60^\circ$) and the lengths of two sides: one side is $12$ (opposite the angle) and the other side is $6$ (which we will use along with the angle to find $x$).

2. Use the Law of Sines

We can employ the Law of Sines which states:

$$ \frac{a}{\sin A} = \frac{b}{\sin B} $$

Here, we need to find the angle opposite side $x$ (let's call it angle $A$). We already have one angle ($60^\circ$) and its opposite side ($12$), so we can write:

$$ \frac{x}{\sin(60^\circ)} = \frac{12}{\sin(60^\circ + B)} $$

3. Find the Missing Angle

Since the sum of angles in a triangle is $180^\circ$, we can find angle $B$:

$$ B = 180^\circ - 60^\circ - C $$

However, we need to find the angle opposite $6$ for simplification in this case.

4. Calculate Using the Values

Let's substitute values using the Law of Sines:

• Knowing that $\sin(60^\circ) = \frac{\sqrt{3}}{2}$, we get:

$$ \frac{6}{\sin(60^\circ)} = \frac{12}{\sin(60^\circ + B)} $$

Solve for $x$:

$$ x = 12 \cdot \frac{\sin(60^\circ)}{6} $$

5. Final Calculation

Substituting $\sin(60^\circ)$:

$$ x = 12 \cdot \frac{\frac{\sqrt{3}}{2}}{6} = 12 \cdot \frac{\sqrt{3}}{12} = \sqrt{3} $$

Now simplify the answer if needed.