In the triangle provided, with angles (3x)°, (3x)°, and (2y - 6)° and a side of 8 in, find the values of x and y.
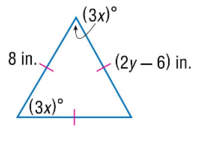
Understand the Problem
The question provides a triangle with certain angles and side lengths expressed in terms of variables. It asks to analyze or solve for those variables based on the properties of triangles, potentially relating to the sum of angles or sides.
Answer
$y = 93 - 3x$
Answer for screen readers
The expressions for the variables are:
- $y = 93 - 3x$
Steps to Solve
-
Identify the Angle Sum Property The sum of the angles in a triangle is always $180^\circ$. Therefore, we can write the equation: $$ (3x) + (3x) + (2y - 6) = 180 $$
-
Combine Like Terms Combine the terms involving $x$ and arrange the equation: $$ 6x + 2y - 6 = 180 $$
-
Simplify the Equation Rearranging and simplifying gives us: $$ 6x + 2y = 186 $$
-
Express $y$ in terms of $x$ To isolate $y$, we can manipulate the equation: $$ 2y = 186 - 6x $$ $$ y = 93 - 3x $$
-
Use the Given Side Lengths We also consider the sides of the triangle. The lengths submitted are relevant for checking the triangle's validity if necessary – in this case, no equation is formed directly from lengths.
The expressions for the variables are:
- $y = 93 - 3x$
More Information
In a triangle, the relationships between angles and sides are crucial. Here, we derived an expression for $y$ based on the angle relationships without needing the lengths of the triangle's sides since the information about angles alone suffices.
Tips
Common mistakes include:
- Forgetting that the sum of angles is $180^\circ$.
- Incorrectly combining terms, leading to wrong coefficients.
- Not isolating variables accurately, which can lead to confusion in further calculations.
AI-generated content may contain errors. Please verify critical information