In the given diagram, find the value of 'a' using the angles represented in terms of 'a'.
Understand the Problem
The question involves a geometric figure with angles expressed in terms of a variable 'a'. We are likely tasked with finding the value of 'a' or solving an equation involving these angles, possibly based on the property that the sum of angles in a polygon is related or equal to some specific value.
Answer
The value of $a$ is $78$.
Answer for screen readers
The value of $a$ is $78$.
Steps to Solve
- Identify the Sum of Angles in the Figure
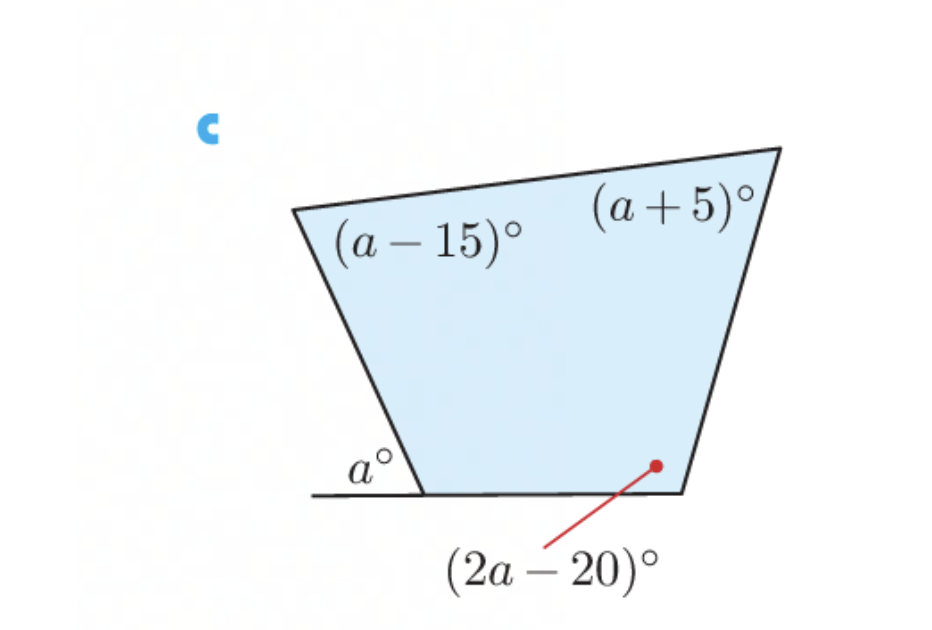
In the given figure, we can identify that the angles form a closed shape (a trapezoid). The sum of the interior angles in any quadrilateral is $360^\circ$.
- Set Up the Equation
The angles in the figure are expressed as follows:
- Angle 1: $(a - 15)^\circ$
- Angle 2: $a^\circ$
- Angle 3: $(2a - 20)^\circ$
- Angle 4: $(a + 5)^\circ$
We set up the equation as follows: $$(a - 15) + a + (2a - 20) + (a + 5) = 360$$
- Combine Like Terms
Now simplify the left-hand side: $$a - 15 + a + 2a - 20 + a + 5 = 360$$
Combine the variables and constants: $$5a - 30 = 360$$
- Solve for 'a'
Next, isolate the variable 'a': $$5a = 360 + 30$$
Which simplifies to: $$5a = 390$$
Now divide both sides by 5: $$a = \frac{390}{5}$$
- Calculate the Value of 'a'
Finally, compute the division: $$a = 78$$
The value of $a$ is $78$.
More Information
In the context of geometry, this problem showcases how to apply the properties of angles in polygons, specifically using the sum of angles in quadrilaterals to find unknown variables.
Tips
- Forgetting to sum all angles: It's important to ensure that all given angles in the figure are included in the equation.
- Miscalculating the constants: Be careful with arithmetic when combining like terms to avoid errors.
AI-generated content may contain errors. Please verify critical information