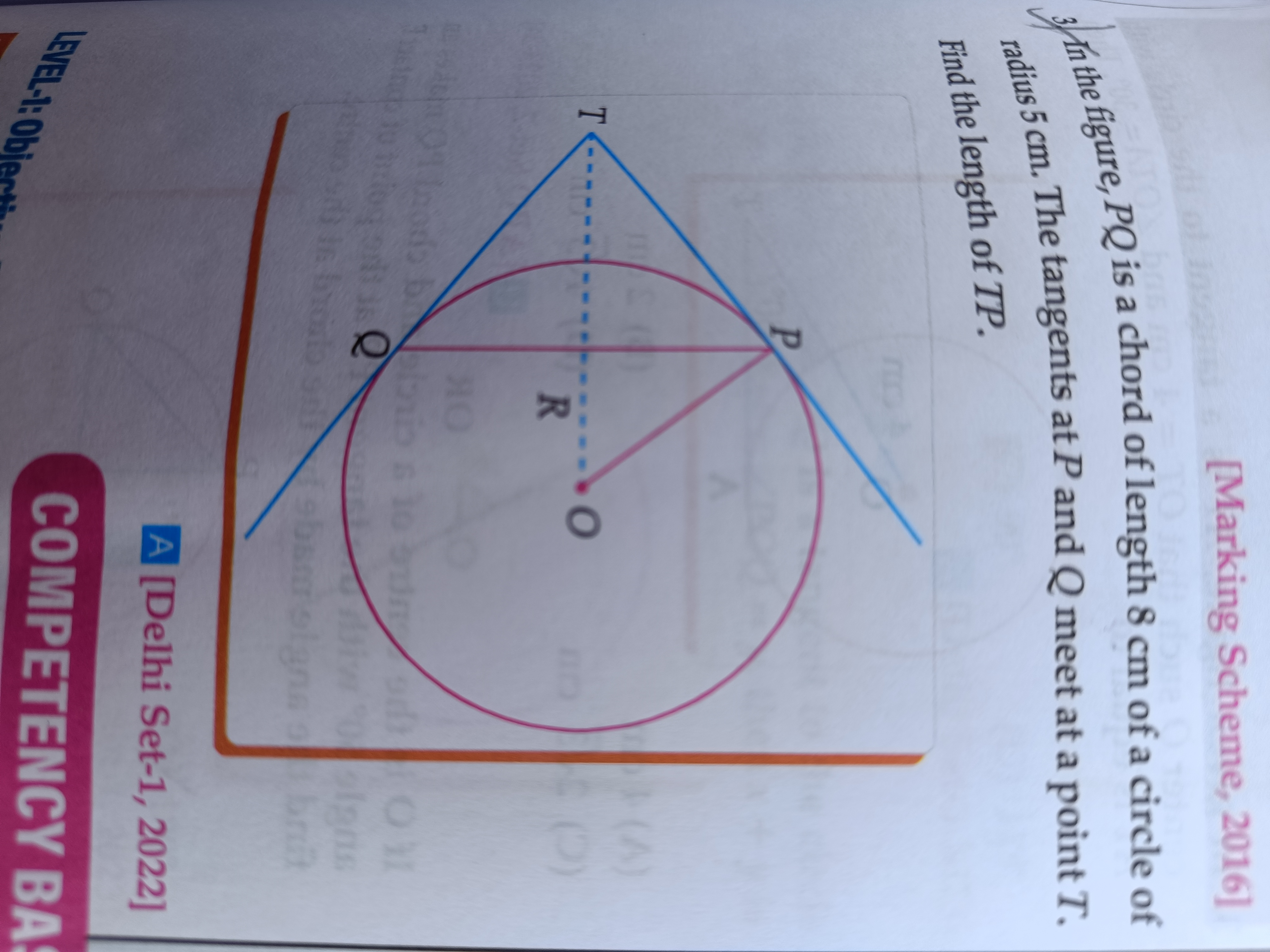
In the figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.
Understand the Problem
The question is asking to find the length of segment TP, given that PQ is a chord of a circle with a specific radius, and tangents are drawn from points P and Q to a point T. We will need to use the properties of tangents and chords in a circle to solve for TP.
Answer
The length of segment $TP$ is $ \sqrt{34} \, \text{cm} $.
Answer for screen readers
The length of segment $TP$ is $ \sqrt{34} , \text{cm} $.
Steps to Solve
- Identify key elements of the problem
In the given problem, we have a circle with radius $r = 5$ cm and a chord $PQ$ of length $8$ cm. Tangents from points $P$ and $Q$ meet at point $T$.
- Use properties of tangents and chords
The key property here is that the lengths of the tangents drawn from an external point to a circle are equal. Thus, we can denote the lengths of the tangents from $T$ to points $P$ and $Q$ as $TP$ and $TQ$, respectively, such that: $$ TP = TQ $$
- Find the length of segment $OP$
The line segment $OP$ is the radius from the center $O$ to point $P$. Since $PQ$ is a chord, we can find the distance from the center $O$ to the chord $PQ$ using the following formula: $$ OP = \sqrt{r^2 - \left(\frac{PQ}{2}\right)^2} $$
Substituting the values:
- $r = 5$ cm
- $PQ = 8$ cm
Calculate: $$ OP = \sqrt{5^2 - \left(\frac{8}{2}\right)^2} $$ $$ OP = \sqrt{25 - 16} $$ $$ OP = \sqrt{9} = 3 \text{ cm} $$
- Use right triangle properties
In triangle $OTQ$, using the Pythagorean theorem, we have: $$ TQ^2 = OP^2 + OQ^2 $$
Since $OQ = OP = 3$ cm, and we have already established that $TP = TQ$, let's denote $TP = x$. Thus: $$ x^2 = 3^2 + 5^2 $$ $$ x^2 = 9 + 25 $$ $$ x^2 = 34 $$
- Calculate the length of segment $TP$
Taking the square root: $$ TP = \sqrt{34} $$
This provides the required length of segment $TP$.
The length of segment $TP$ is $ \sqrt{34} , \text{cm} $.
More Information
The chord length and radius in connection with tangents allows us to derive various lengths within the circle. Using properties of tangents and the Pythagorean theorem helps in solving geometric problems efficiently.
Tips
- A common mistake is neglecting the equality of tangents from point $T$. Always remember that $TP$ equals $TQ$.
- Misapplying the Pythagorean theorem by not properly identifying which sides correspond to the triangle can lead to incorrect results.
AI-generated content may contain errors. Please verify critical information