أوجد قيمة cscθ إذا كان tanθ > 0 وsecθ = -6/5.
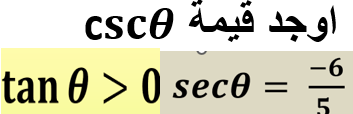
Understand the Problem
السؤال يطلب منا إيجاد قيمة دالة cscθ بناءً على المعلومات المعطاة مثل أن tanθ > 0 وأن secθ = -6/5. سنقيم العلاقات بين الدوال المثلثية لحل المسألة.
Answer
$$ cscθ = \frac{6}{\sqrt{11}} $$
Answer for screen readers
$$ cscθ = \frac{6}{\sqrt{11}} $$
Steps to Solve
- فهم القيم المعطاة
نعلم أن $secθ = -\frac{6}{5}$. وبما أن $secθ = \frac{1}{cosθ}$، يمكننا استنتاج قيمة $cosθ$:
$$ cosθ = -\frac{5}{6} $$
- تحديد الربع المناسب
نظرًا لأن $secθ$ سالب و $tanθ$ موجب، فهذا يعني أننا في الربع الثاني حيث $cosθ < 0$ و $sinθ > 0$.
- استخدام معادلة فيثاغورس
يمكننا استخدام معادلة فيثاغورس لإيجاد $sinθ$. نستخدم العلاقة:
$$ sin^2θ + cos^2θ = 1 $$
نستبدل $cosθ$:
$$ sin^2θ + \left(-\frac{5}{6}\right)^2 = 1 $$
- تبسيط المعادلة
نقوم بتبسيط المعادلة:
$$ sin^2θ + \frac{25}{36} = 1 $$
$$ sin^2θ = 1 - \frac{25}{36} $$
$$ sin^2θ = \frac{36}{36} - \frac{25}{36} = \frac{11}{36} $$
- إيجاد قيمة sinθ
نأخذ الجذر التربيعي:
$$ sinθ = \sqrt{\frac{11}{36}} = \frac{\sqrt{11}}{6} $$
- حساب قيمة cscθ
نعلم أن:
$$ cscθ = \frac{1}{sinθ} $$
لذلك:
$$ cscθ = \frac{1}{\frac{\sqrt{11}}{6}} = \frac{6}{\sqrt{11}} $$
$$ cscθ = \frac{6}{\sqrt{11}} $$
More Information
تمثل دالة cscθ المعكوس للدالة sinθ. بما أن $secθ$ هنا سالب و$tanθ$ موجب، هذا يشير إلى أن الزاوية θ تقع في الربع الثاني.
Tips
- عدم معرفة أن $secθ$ سالب يجب أن تقودنا إلى الربع الثاني.
- الخطأ في حساب $sin^2θ$ أو في الجذر التربيعي مما قد يؤدي لأخطاء في قيمته النهائية.
AI-generated content may contain errors. Please verify critical information