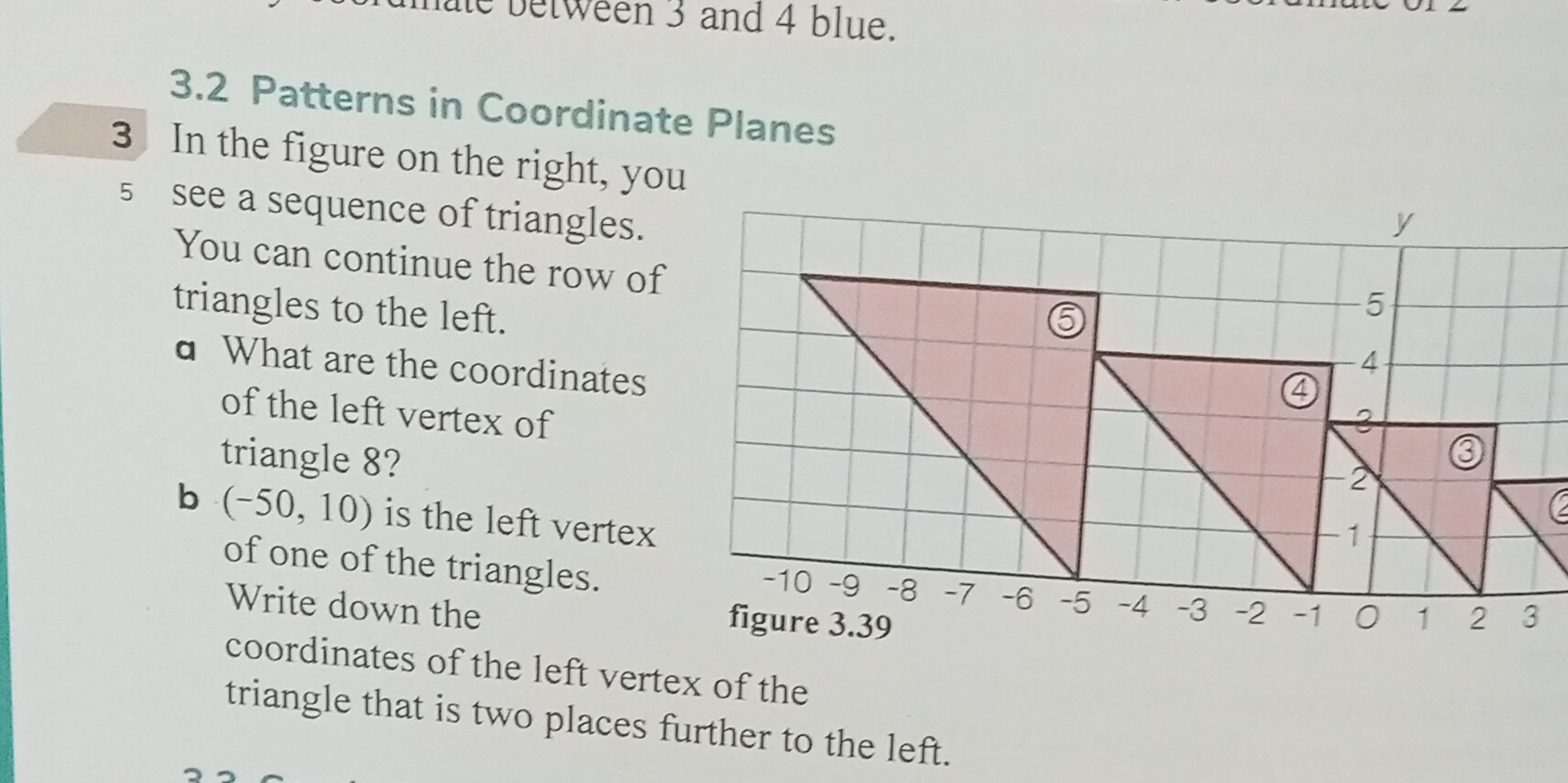
In the figure on the right, you see a sequence of triangles. You can continue the row of triangles to the left. a) What are the coordinates of the left vertex of triangle 8? b) (-5... In the figure on the right, you see a sequence of triangles. You can continue the row of triangles to the left. a) What are the coordinates of the left vertex of triangle 8? b) (-50, 10) is the left vertex of one of the triangles. Write down the coordinates of the left vertex of the triangle that is two places further to the left.
Understand the Problem
The question asks for the coordinates of the left vertex of triangle 8 based on a provided sequence of triangles. Additionally, it requires determining the coordinates of another vertex given specific information about another triangle's vertex.
Answer
The coordinates of triangle 8's left vertex are $(-2, 4)$, and the other vertex is $(-52, 10)$.
Answer for screen readers
The coordinates of the left vertex of triangle 8 are $(-2, 4)$.
The coordinates of the left vertex of the triangle that is two places further to the left from $(-50, 10)$ are $(-52, 10)$.
Steps to Solve
-
Identify the pattern in the triangles' coordinates
Looking at the provided image, we can observe the left vertices of the triangles. The left vertices of triangles 5, 4, 3, 2, and 1 are located at $(-5, 2)$, $(-6, 4)$, $(-7, 2)$, $(-8, 4)$, and $(-9, 2)$ respectively, clearly alternating their positions along the y-coordinate. -
Determine the coordinates of triangle 6
Following the same pattern, triangle 6 would have its left vertex at $(-4, 4)$.
Triangle 7 will follow at $(-3, 2)$ and, finally, triangle 8 will have its left vertex at $(-2, 4)$. -
Write down the coordinates for triangle 8
Thus, the coordinates of the left vertex of triangle 8 are $(-2, 4)$. -
Find coordinates for part b
For part b, we start with the coordinates of the left vertex of a triangle given as $(-50, 10)$. Since we need the coordinates two places further to the left, we will subtract 2 from the x-coordinate.
So, the new coordinates will be $(-50 - 2, 10)$, which equals $(-52, 10)$.
The coordinates of the left vertex of triangle 8 are $(-2, 4)$.
The coordinates of the left vertex of the triangle that is two places further to the left from $(-50, 10)$ are $(-52, 10)$.
More Information
The sequence of triangles follows a repeating pattern where the x-coordinates gradually decrease and the y-coordinates alternate between two values (2 and 4). This pattern can help identify the coordinates of any triangle in the sequence.
Tips
- Overlooking the pattern: Some might not notice the alternating pattern in y-coordinates, which can lead to incorrect conclusions about the coordinates of the triangles.
- Misinterpreting left movements: When calculating how far left to go, it’s crucial to remember that left means subtracting from the x-coordinate, not adding.
AI-generated content may contain errors. Please verify critical information