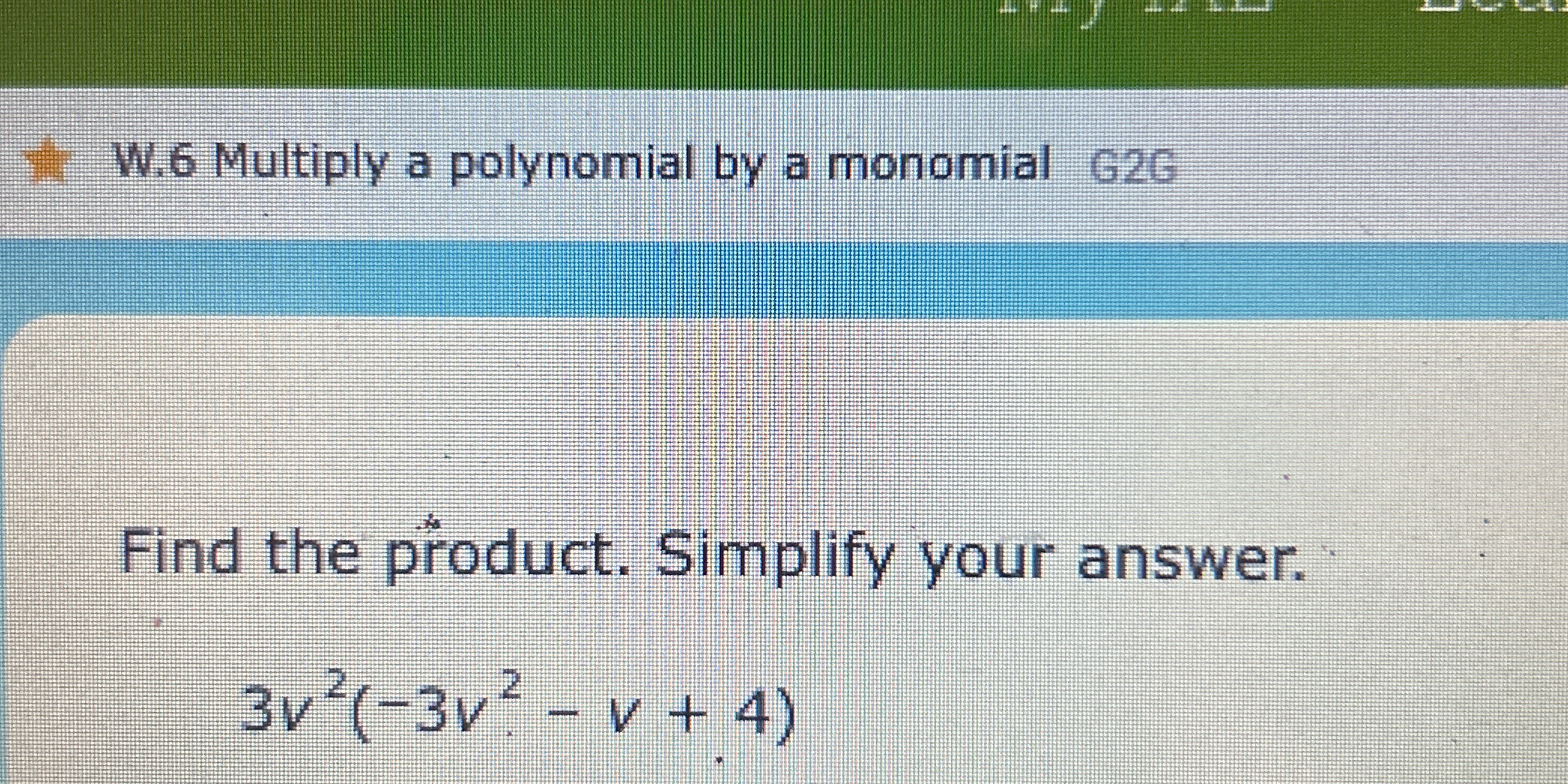
Find the product. Simplify your answer: 3v²(-3v² - v + 4)
Understand the Problem
The question is asking to find the product of the given polynomial expression and then simplify the result. Specifically, it's multiplying the monomial 3v² by the polynomial (-3v² - v + 4).
Answer
The simplified product is: $-9v^4 - 3v^3 + 12v^2$.
Answer for screen readers
The simplified product is:
$$ -9v^4 - 3v^3 + 12v^2 $$
Steps to Solve
-
Write down the expression
The expression to multiply is:
$$ 3v^2 \cdot (-3v^2 - v + 4) $$ -
Distribute the monomial
Multiply the monomial $3v^2$ by each term inside the parentheses:
- For the first term:
$$ 3v^2 \cdot (-3v^2) = -9v^4 $$ - For the second term:
$$ 3v^2 \cdot (-v) = -3v^3 $$ - For the third term:
$$ 3v^2 \cdot 4 = 12v^2 $$
-
Combine the results
Now combine all the terms we calculated:
$$ -9v^4 - 3v^3 + 12v^2 $$ -
Write the final simplified expression
The final result is:
$$ -9v^4 - 3v^3 + 12v^2 $$
The simplified product is:
$$ -9v^4 - 3v^3 + 12v^2 $$
More Information
When multiplying a monomial by a polynomial, each term in the polynomial is multiplied by the monomial. This results in a new polynomial formed by the sum of all the products. This process is called distribution.
Tips
- Not distributing the monomial to each term in the polynomial correctly.
- Forgetting to carry the sign of the terms during multiplication (e.g., multiplying a negative term and forgetting it changes the sign).
AI-generated content may contain errors. Please verify critical information