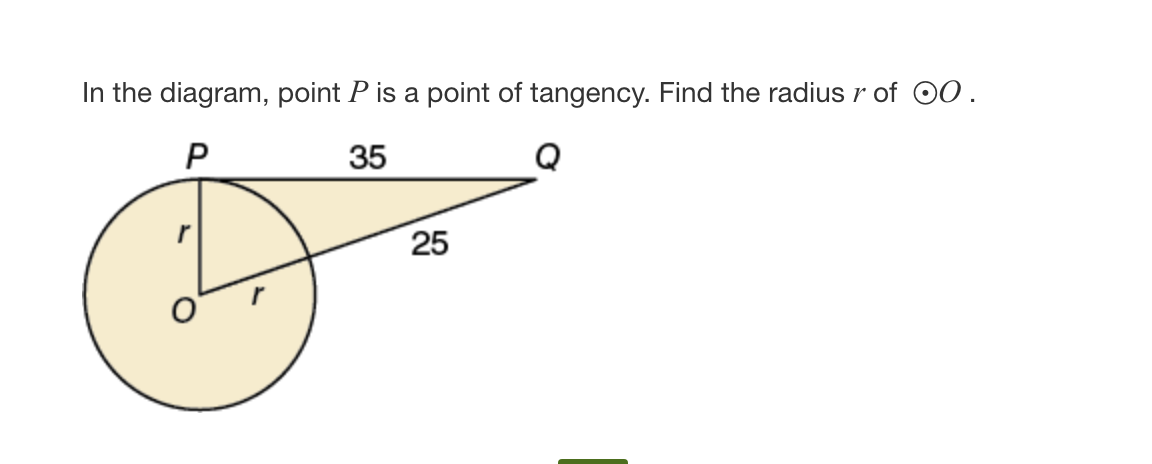
In the diagram, point P is a point of tangency. Find the radius r of OO.
Understand the Problem
The question is asking us to find the radius 'r' of the circle given a diagram involving tangents and segments. It requires applying geometric concepts related to tangents and circles.
Answer
The radius \( r \) of the circle is \( 12 \).
Answer for screen readers
The radius ( r ) of the circle is ( 12 ).
Steps to Solve
-
Identify the triangle formed We have a right triangle OPQ, where OP is the radius $r$, PQ is the tangent, and OQ is the hypotenuse. PQ is 35 and OQ is 25.
-
Apply the Pythagorean theorem Using the Pythagorean theorem which states that in a right triangle, $a^2 + b^2 = c^2$, where $c$ is the hypotenuse, we can express it as: $$ r^2 + 35^2 = (25 + r)^2 $$
-
Expand and simplify the equation Expanding both sides: $$ r^2 + 1225 = 625 + 50r + r^2 $$ Now, we can eliminate $r^2$ from both sides.
-
Rearrange the equation Rearranging the equation gives: $$ 1225 - 625 = 50r $$ This simplifies to: $$ 600 = 50r $$
-
Solve for r Dividing both sides by 50: $$ r = \frac{600}{50} = 12 $$
The radius ( r ) of the circle is ( 12 ).
More Information
The problem involved geometry concepts relating to tangent lines and right triangles. The radius can be determined using the Pythagorean theorem.
Tips
- Forgetting to apply the Pythagorean theorem correctly, leading to incorrect assumptions about the relationships in the triangle.
- Miscalculating the expansion or simplification of the equation.
AI-generated content may contain errors. Please verify critical information