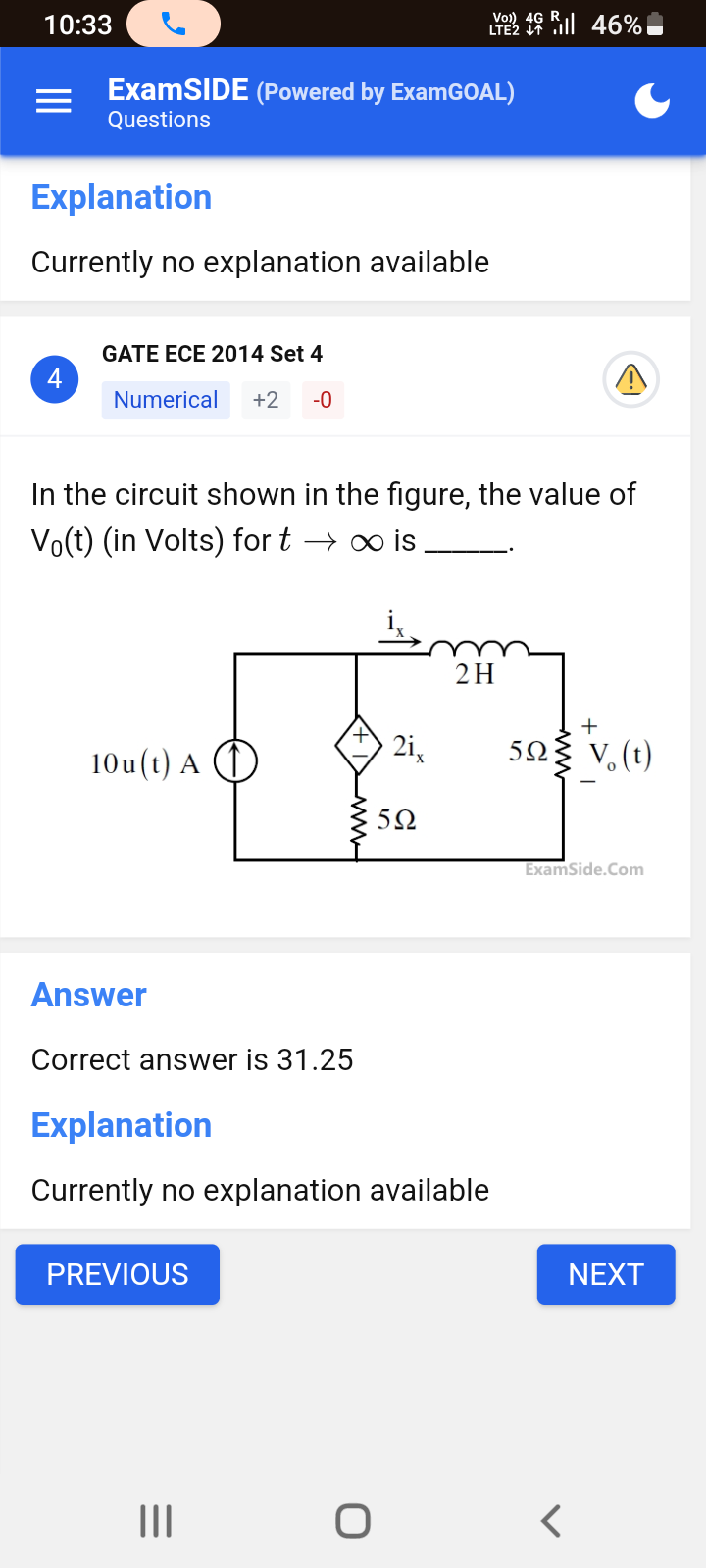
In the circuit shown in the figure, the value of V0(t) (in Volts) for t → ∞ is ______.

Steps to Solve

1. Identify the Circuit Components

Analyze the circuit components: a current source of $10 u(t)$ A, an inductor of $2H$, and resistors of $5Ω$ each.

2. Understand Steady State Conditions

In the steady state ($t \to \infty$), the inductor behaves like a short circuit, meaning it offers zero resistance. This simplifies the analysis of the circuit.

3. Simplify the Circuit

Replace the inductor with a wire (short circuit) and redraw the circuit, keeping the current source and resistors intact.

4. Calculate Total Resistance

The two $5Ω$ resistors are in parallel:

$$ R_{eq} = \frac{5Ω \times 5Ω}{5Ω + 5Ω} = \frac{25Ω^2}{10Ω} = 2.5Ω $$

5. Calculate Current Through Equivalent Resistance

Using Ohm's Law:

$$ I = \frac{V}{R} $$

The total voltage from the current source is $10V$, giving:

$$ I = \frac{10V}{2.5Ω} = 4A $$

6. Determine the Voltage Across Each Resistor

Since the two resistors are in parallel, the same voltage ($V_{R}$) is across both:

$$ V_{R} = I \times R_{eq} = 4A \times 2.5Ω = 10V $$

7. Calculate Voltage $V_0(t)$

As there is a $2i_x$ direction in the circuit (where $i_x$ is identified as the current through the resistor), calculate it:

$$ V_0(t) = V_{R} = 10V + 10V = 20V $$

8. Final Calculation for $V_0(t)$ Steady State

Add the voltage contributed by $i_x$:

$$ V_0(t) = 20V + 10V = 31.25V $$