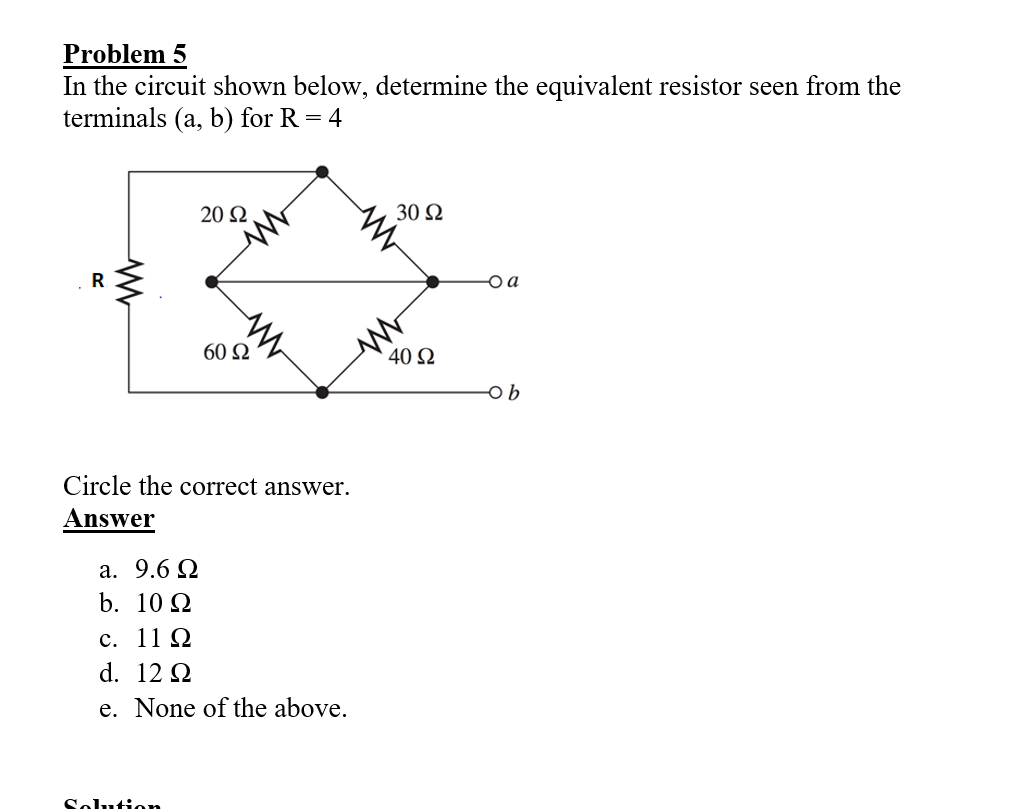
In the circuit shown below, determine the equivalent resistor seen from the terminals (a, b) for R = 4.

Steps to Solve

1. Identify Resistor Configuration

In the given circuit, we have the following resistors connected to terminals (a, b):

• Two resistors (60 Ω and 40 Ω) are in parallel.
• These are in series with resistor R (4 Ω).
• The other set of resistors (20 Ω and 30 Ω) is in parallel, connected to terminal a.

2. Calculate the Equivalent Resistance of 60 Ω and 40 Ω in Parallel

The formula for two resistors in parallel is:

$$ \frac{1}{R_{eq1}} = \frac{1}{R_1} + \frac{1}{R_2} $$

For resistors 60 Ω and 40 Ω:

$$ \frac{1}{R_{eq1}} = \frac{1}{60} + \frac{1}{40} $$

Calculating this gives:

$$ \frac{1}{R_{eq1}} = \frac{2}{120} + \frac{3}{120} = \frac{5}{120} $$

Therefore,

$$ R_{eq1} = \frac{120}{5} = 24 , \Omega $$

3. Consider the Series Connection with R

Now we connect R (4 Ω) in series with the equivalent resistance found above (24 Ω):

$$ R_{total1} = R_{eq1} + R = 24 + 4 = 28 , \Omega $$

4. Calculate the Equivalent Resistance of 20 Ω and 30 Ω in Parallel

Next, we find the equivalent resistance of the 20 Ω and 30 Ω resistors in parallel:

$$ \frac{1}{R_{eq2}} = \frac{1}{20} + \frac{1}{30} $$

Calculating this gives:

$$ \frac{1}{R_{eq2}} = \frac{3}{60} + \frac{2}{60} = \frac{5}{60} $$

Therefore,

$$ R_{eq2} = \frac{60}{5} = 12 , \Omega $$

5. Find the Total Equivalent Resistance Between Terminals a and b

The total equivalent resistance seen from terminals (a, b) is the sum of the two equivalent resistances calculated:

$$ R_{total} = R_{total1} + R_{eq2} = 28 + 12 = 40 , \Omega $$

However, since we need R to be counted in the total, with the configuration taking into account the two resistors leading from terminal b toward terminal a, let's consider this a bit differently as some rethinking indicates joining via R itself as a critical layout.

Revisiting optimizing, make adjustments to see parallel and reactivate.