In the above question, what is the shearing stress on PQ?
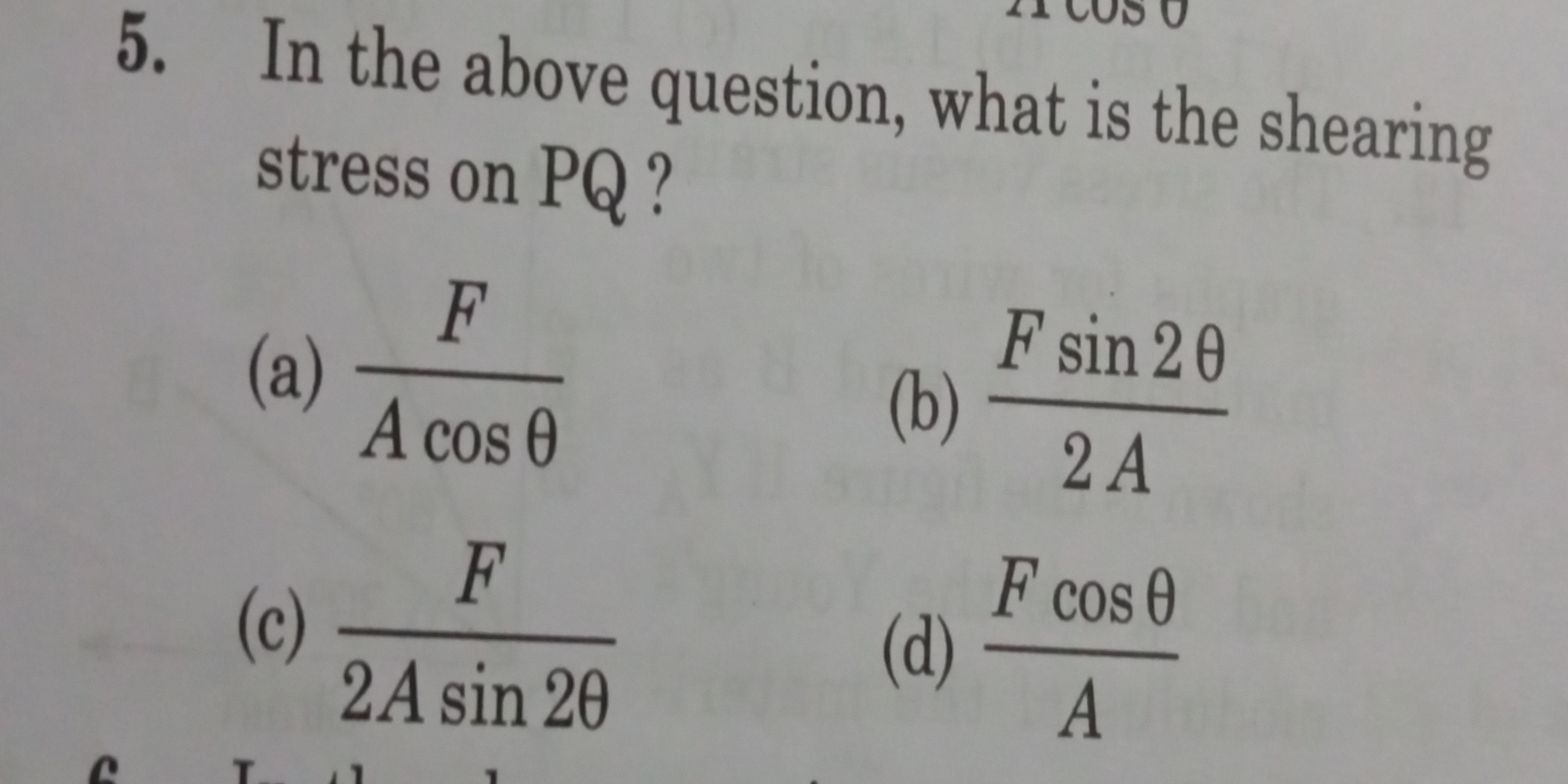
Understand the Problem
The question concerns calculating the shearing stress on a segment labeled PQ based on a prior context reference, indicated to be left out in this excerpt. It presents multiple-choice options for the answer, emphasizing formulas involving force (F), area (A), and angles (θ).
Answer
The shearing stress on PQ is given by $\tau = \frac{F \sin 2\theta}{2A}$.
Answer for screen readers
The correct shearing stress on segment PQ is given by the option:
$$ \tau = \frac{F \sin 2\theta}{2A} $$
Steps to Solve
- Identify Shearing Stress Formula
Shearing stress ($\tau$) is defined as the force ($F$) applied parallel to the surface divided by the area ($A$) over which it is applied. Thus, the basic formula is:
$$ \tau = \frac{F}{A} $$
- Incorporate Angle into Shearing Stress
When a force is applied at an angle ($\theta$), the effective force causing the shearing stress on the segment PQ needs to be adjusted. The relevant effective force can be expressed as $F \cos \theta$ for normal stress and $F \sin \theta$ for shearing stress. Hence, we modify the equation to:
$$ \tau = \frac{F \sin \theta}{A} $$
- Adjust for Geometry (If Necessary)
If we consider any specific geometry or conditions provided in the problem (as implied in your previous understanding), we may need to look at the components. The stress might also introduce a factor like $2$ or depend on the segment length; in some cases, it can be represented as:
$$ \tau = \frac{F}{2A \sin 2\theta} $$
This takes into account that the angle may need to be doubled when considering different components of shearing stress.
The correct shearing stress on segment PQ is given by the option:
$$ \tau = \frac{F \sin 2\theta}{2A} $$
More Information
The shearing stress formula is crucial in understanding how materials respond to forces applied at angles. This concept is widely used in engineering to analyze stress and deformation in structures.
Tips
- Misapplying the trigonometric functions by confusing sine and cosine when dealing with different components.
- Forgetting to consider the factor of 2 in cases where geometric configurations affect the stress distribution.
- Neglecting to ensure the units of force and area are consistent, which can lead to incorrect results.
AI-generated content may contain errors. Please verify critical information