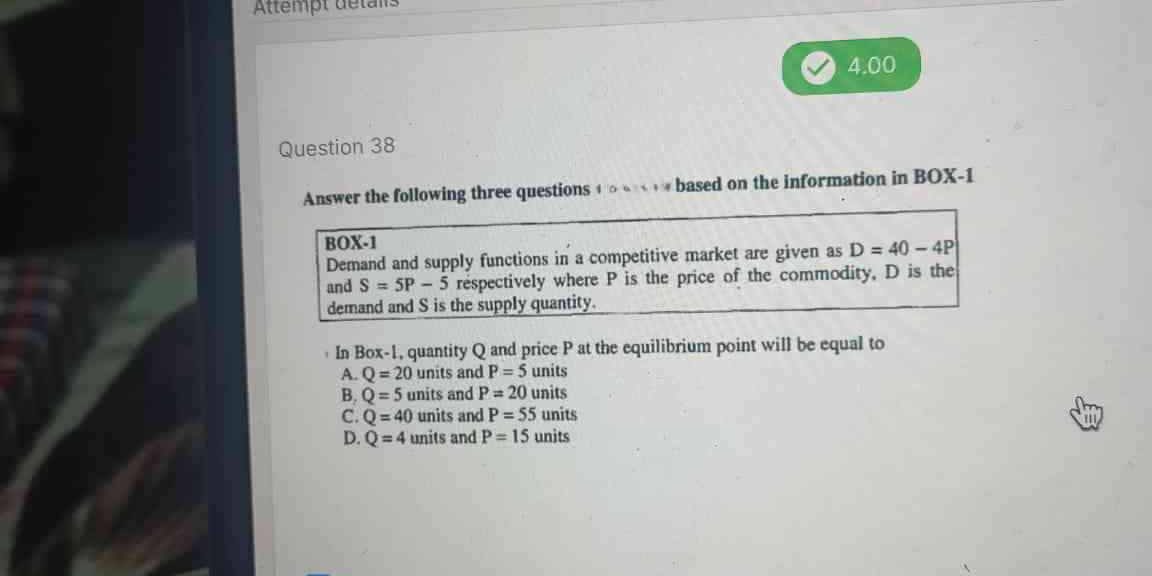
In Box-1, quantity Q and price P at the equilibrium point will be equal to A. Q=20 units and P=5 units B. Q=5 units and P=20 units C. Q=40 units and P=55 units D. Q=4 units and P=1... In Box-1, quantity Q and price P at the equilibrium point will be equal to A. Q=20 units and P=5 units B. Q=5 units and P=20 units C. Q=40 units and P=55 units D. Q=4 units and P=15 units
Understand the Problem
The question is asking to determine the equilibrium quantity (Q) and price (P) based on the demand and supply equations given. We need to find the correct values from the options provided by equating the demand and supply functions.
Answer
Q = 20, P = 5
Answer for screen readers
The equilibrium quantity (Q) is 20 units, and the price (P) is 5 units, i.e., (Q = 20) and (P = 5).
Steps to Solve
-
Set the Demand Equal to Supply To find the equilibrium quantity (Q) and price (P), we need to set the demand function equal to the supply function. So we have: $$ 40 - 4P = 5P - 5 $$
-
Rearrange the Equation Now, we'll rearrange the equation to isolate (P): $$ 40 + 5 = 5P + 4P $$ Which simplifies to: $$ 45 = 9P $$
-
Solve for Price (P) Next, we divide both sides by 9 to find (P): $$ P = \frac{45}{9} = 5 $$
-
Substitute P Back to Find Q Now substitute (P = 5) back into either the demand or supply equation to calculate (Q). We'll use the demand equation: $$ D = 40 - 4(5) $$ $$ D = 40 - 20 = 20 $$
Thus, (Q = 20) units.
- Conclusion of Equilibrium Point The equilibrium price is (P = 5) and the equilibrium quantity is (Q = 20).
The equilibrium quantity (Q) is 20 units, and the price (P) is 5 units, i.e., (Q = 20) and (P = 5).
More Information
In a competitive market, the equilibrium point is where the quantity demanded equals the quantity supplied, which helps determine the market price and quantity of goods traded.
Tips
- A common mistake is to misinterpret the supply equation or to forget to set demand equal to supply properly. Always double-check your algebra.
AI-generated content may contain errors. Please verify critical information