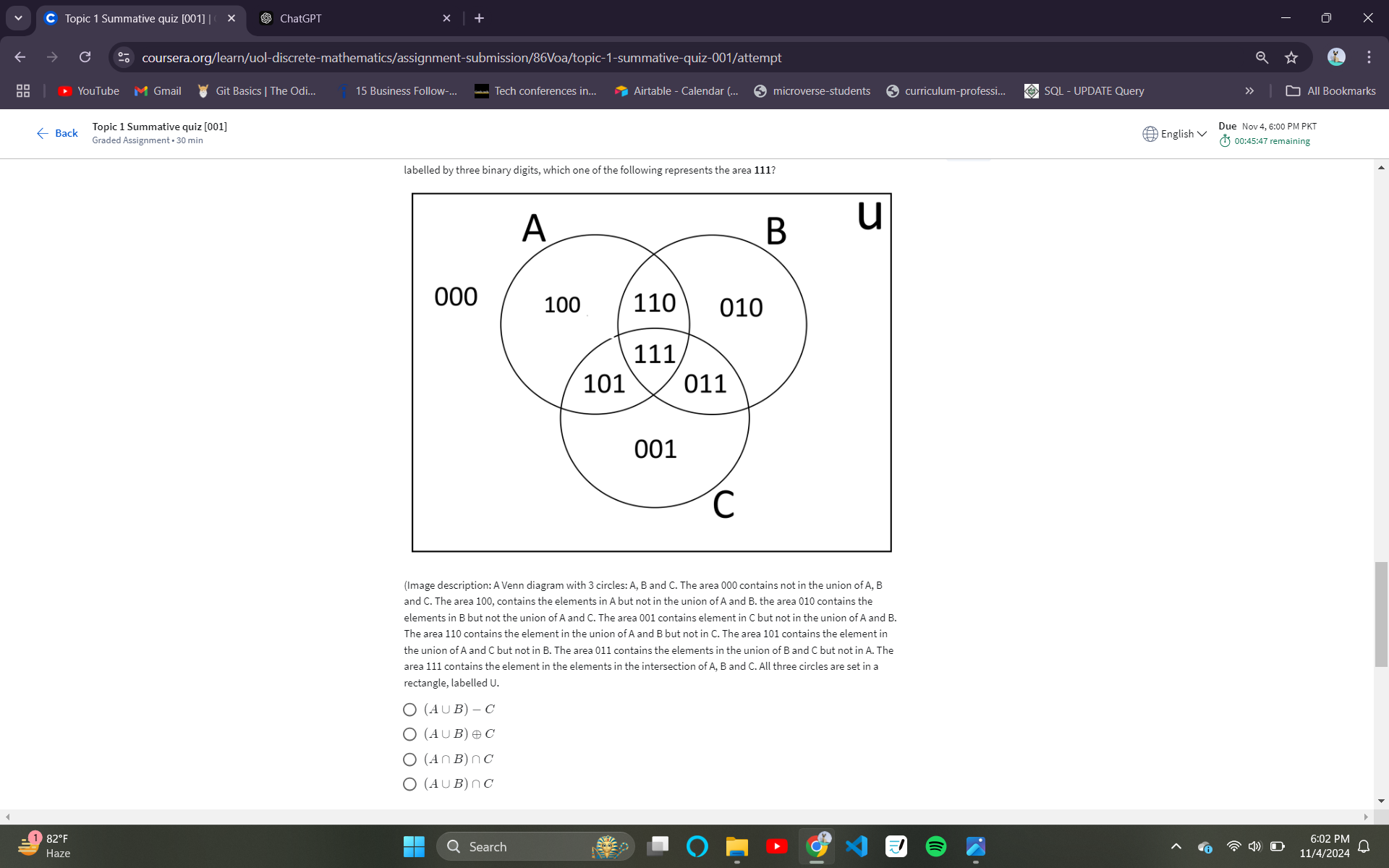
In a Venn diagram labeled by three binary digits, which one of the following represents the area 111?
Understand the Problem
The question involves a Venn diagram with three sets labeled A, B, and C, and asks which expression correctly represents the area labeled '111' in the context of the sets. The objective is to analyze the Venn diagram and identify the logical set operation that corresponds to the intersection of the sets represented by the binary digits.
Answer
The area '111' is represented by $A \cap B \cap C$.
Answer for screen readers
The correct expression representing the area labeled '111' is $A \cap B \cap C$.
Steps to Solve
-
Identify the Area '111' The area labeled '111' corresponds to the elements that are in all three sets A, B, and C. This indicates the intersection of the sets A, B, and C.
-
Understand Set Operations The expression representing the area '111' must reflect the intersection of A, B, and C. We use the intersection symbol $\cap$ to represent this operation. The expression can be written as: $$ A \cap B \cap C $$
-
Analyze the Multiple Choice Options Evaluate the given options to find the correct expression. The correct representation for the area '111' should indicate that we consider only the elements common to A, B, and C, which is simply $A \cap B \cap C$.
-
Select the Correct Answer Among the choices, we should look for an expression that correctly uses the intersection operation as stated. The correct answer for the area '111' is: $$ A \cap B \cap C $$ or an equivalent expression that denotes this intersection.
The correct expression representing the area labeled '111' is $A \cap B \cap C$.
More Information
The area labeled '111' in a Venn diagram signifies the common elements shared by the three sets A, B, and C. Understanding basic set operations and Venn diagrams is essential for interpreting these kinds of problems.
Tips
- Confusing Union and Intersection: A common mistake is to confuse the union ($A \cup B$) with the intersection ($A \cap B$). Make sure to focus on what part of the diagram the label corresponds to.
- Misinterpretation of Labels: It’s crucial to accurately read the binary labels corresponding to each section. Ensure that '111' is recognized as the intersection of all three sets.
AI-generated content may contain errors. Please verify critical information