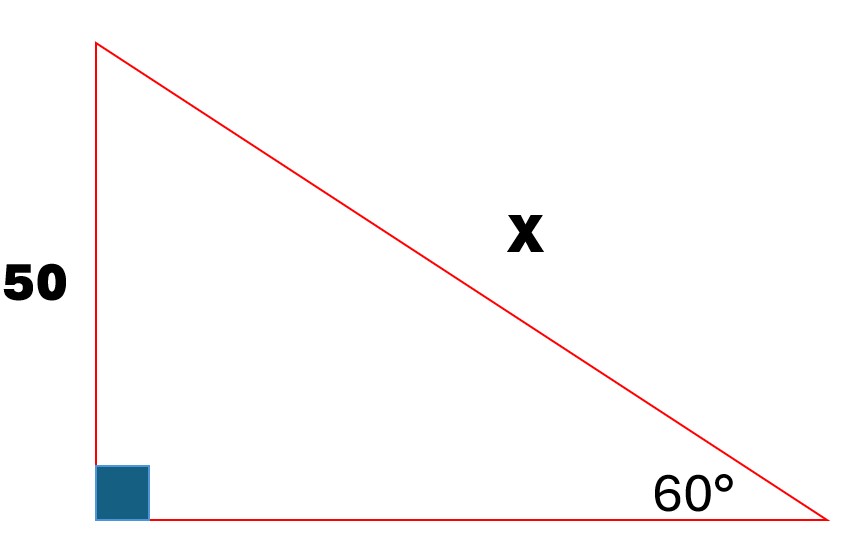
In a right triangle, if one side is 50 and the angle opposite to it is 60 degrees, find the length of side x.
Understand the Problem
The question is asking to find the length of side 'x' in a right triangle where one angle measures 60 degrees and the opposite side has a length of 50. We can use trigonometric ratios to solve for 'x' using the sine function.
Answer
The length of side 'x' is \( x = \frac{100\sqrt{3}}{3} \).
Answer for screen readers
The length of side 'x' is ( x = \frac{100\sqrt{3}}{3} ).
Steps to Solve
- Identify the relevant trigonometric function
In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side to the hypotenuse. For angle $60^\circ$, we can express this as:
$$ \sin(60^\circ) = \frac{\text{opposite}}{\text{hypotenuse}} $$
- Insert the known values into the equation
We know the opposite side (50) and the sine of 60 degrees. The equation becomes:
$$ \sin(60^\circ) = \frac{50}{x} $$
- Solve for the hypotenuse 'x'
First, calculate $\sin(60^\circ)$:
$$ \sin(60^\circ) = \frac{\sqrt{3}}{2} $$
Now substitute this value into the equation:
$$ \frac{\sqrt{3}}{2} = \frac{50}{x} $$
- Cross-multiply and solve for 'x'
Cross-multiplying gives us:
$$ \sqrt{3} \cdot x = 100 $$
Now, solve for 'x':
$$ x = \frac{100}{\sqrt{3}} $$
- Rationalize the denominator (optional)
To express (x) in a simpler form, multiply the numerator and denominator by (\sqrt{3}):
$$ x = \frac{100\sqrt{3}}{3} $$
The length of side 'x' is ( x = \frac{100\sqrt{3}}{3} ).
More Information
The angle of (60^\circ) is significant as it corresponds to a special angle in trigonometry. The sine of this angle, ( \frac{\sqrt{3}}{2} ), is commonly encountered in various trigonometric calculations.
Tips
- Not using the correct trigonometric ratio: Ensure to recognize whether to use sine, cosine, or tangent based on the sides involved.
- Miscalculating the sine value: Always double-check trigonometric values for accuracy.