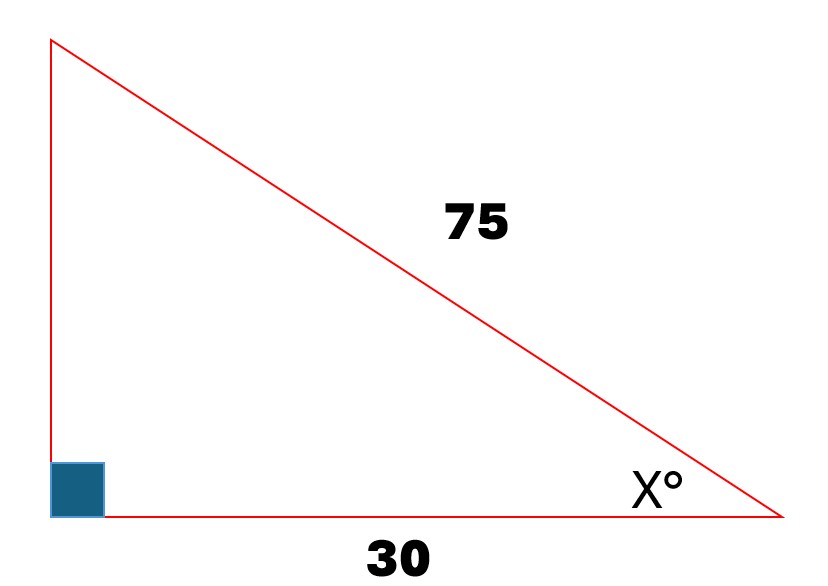
In a right triangle, if one leg is 30 units, the other leg is 75 units, what is the value of angle X?
Understand the Problem
The question involves determining the value of angle X in a right triangle, where the lengths of the sides are given. This requires the application of trigonometric principles, specifically the sine, cosine, or tangent ratios depending on the known sides and the desired angle.
Answer
$X \approx 66.42^\circ$
Answer for screen readers
The value of angle $X$ is approximately $66.42^\circ$.
Steps to Solve
-
Identify the relevant triangle sides In the right triangle, we are given the lengths of the sides: the adjacent side to angle $X$ is 30, and the hypotenuse is 75.
-
Select the appropriate trigonometric function To find angle $X$, we can use the cosine function, which relates the adjacent side and hypotenuse: $$ \cos(X) = \frac{\text{Adjacent}}{\text{Hypotenuse}} $$
-
Set up the equation Plugging the known values into the cosine function: $$ \cos(X) = \frac{30}{75} $$
-
Simplify the ratio Calculate the ratio: $$ \cos(X) = \frac{2}{5} = 0.4 $$
-
Find the angle using the inverse cosine To determine angle $X$, we take the inverse cosine: $$ X = \cos^{-1}(0.4) $$
-
Calculate the angle Using a calculator: $$ X \approx 66.42^\circ $$
The value of angle $X$ is approximately $66.42^\circ$.
More Information
In a right triangle, the angles can be found using trigonometric ratios, which help in many real-world applications, such as architecture and navigation.
Tips
- Confusing the sides: Ensure you identify which side is adjacent and which is the hypotenuse.
- Using the wrong trigonometric function: Remember to use cosine when you have adjacent and hypotenuse values.
AI-generated content may contain errors. Please verify critical information