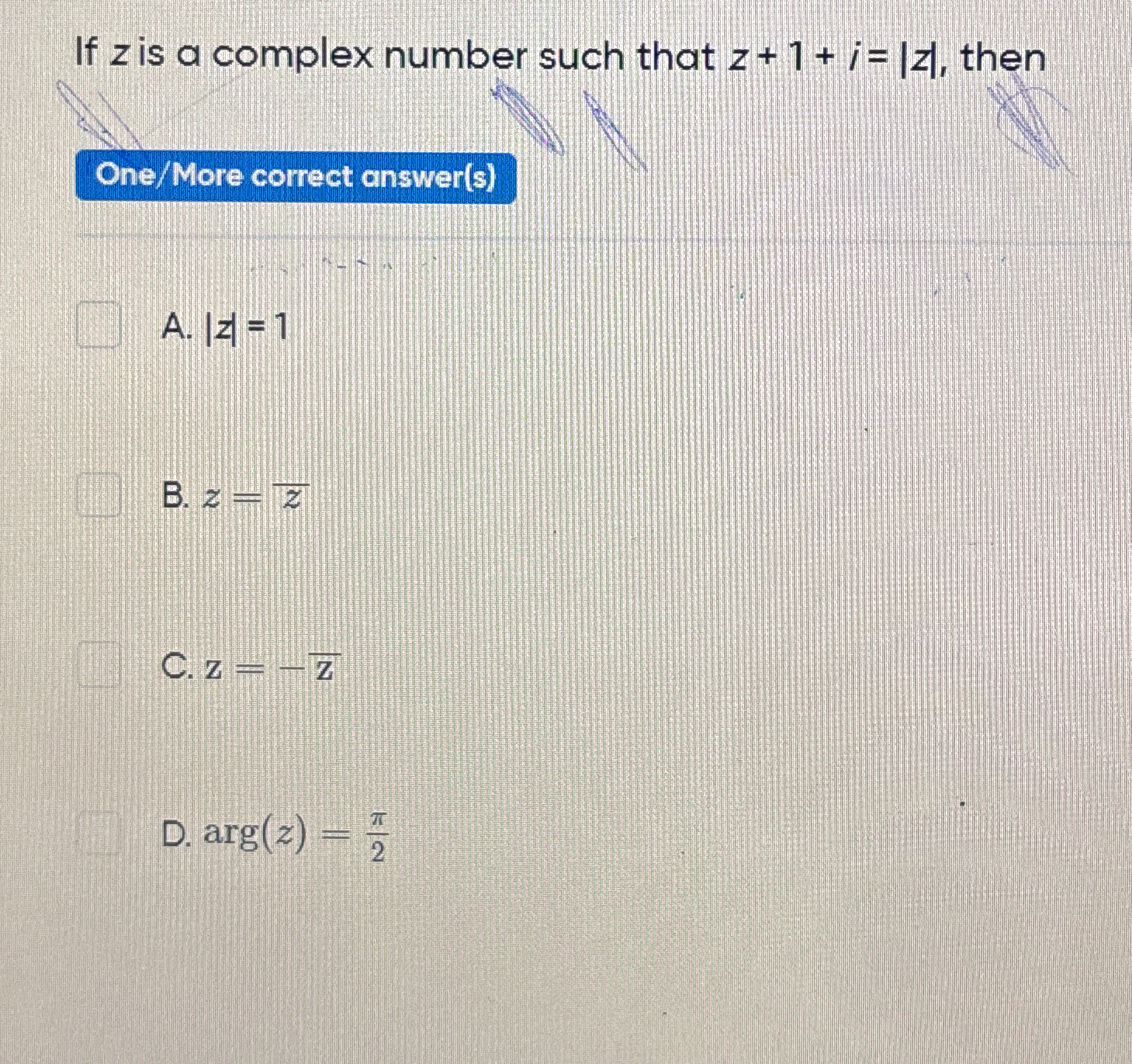
If z is a complex number such that z + 1 + i = |z|, then.

Steps to Solve

1. Rewrite the equation in terms of z The given equation is ( z + 1 + i = |z| ). We can rewrite this as: $$ |z| = z + 1 + i $$

2. Express z in terms of its components Let ( z = x + yi ), where ( x ) is the real part and ( y ) is the imaginary part. Then: $$ |z| = \sqrt{x^2 + y^2} $$ Substituting, we have: $$ \sqrt{x^2 + y^2} = (x + 1) + yi $$

3. Separate real and imaginary parts From the equation, we break it into real and imaginary parts:

   • Real part: ( \sqrt{x^2 + y^2} = x + 1 )
   • Imaginary part: ( 0 = y )

4. Find the values of components Since ( y = 0 ), it follows that ( z = x ) (a real number). The magnitude simplifies to: $$ |z| = |x| $$ Thus, the equation simplifies to: $$ |x| = x + 1 $$

5. Solve for x We can now solve the equation:

   • Case 1: ( x \geq 0 ) gives ( x = x + 1 ), which is a contradiction.
   • Case 2: ( x < 0 ) gives ( -x = x + 1 ) or ( -2x = 1 ). Solving for ( x ) gives: $$ x = -\frac{1}{2} $$ So, ( z = -\frac{1}{2} ).

6. Find the magnitude and argument The magnitude is: $$ |z| = \left| -\frac{1}{2} \right| = \frac{1}{2} $$ The argument, since ( z ) is negative on the real axis, is: $$ \arg(z) = \pi \text{ (or } 180^\circ\text{)} $$