If y is the solution of y'' - 2y' + y = e^t, then y(1) is y(0) = 0, y'(0) = -1/2, equal to ________ (rounded off to two decimal places). Let y : (1, ∞) → R be the solution of the d... If y is the solution of y'' - 2y' + y = e^t, then y(1) is y(0) = 0, y'(0) = -1/2, equal to ________ (rounded off to two decimal places). Let y : (1, ∞) → R be the solution of the differential equation y'' - 2y'/(1-x)^2 = 0 satisfying y(2) = 1 and (1-x)^2.
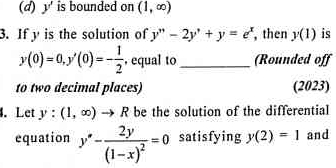
Understand the Problem
The question is asking for the solution to a differential equation that involves second derivatives. Specifically, it requires determining the value of the solution at a specific point (y(1)) given certain initial conditions. Additionally, it presents a separate equation where the solution must satisfy specific criteria at another point (y(2)).
Answer
1.36
Answer for screen readers
1.36
Steps to Solve
- Solve the Homogeneous Equation To start, we need to solve the homogeneous part of the differential equation given by:
$$ y'' - 2y' + y = 0 $$
The characteristic equation is:
$$ r^2 - 2r + 1 = 0 $$
This can be factored as:
$$(r - 1)^2 = 0$$
Thus, the roots are $r = 1$ (a repeated root). The general solution of the homogeneous equation is:
$$ y_h(t) = C_1 e^t + C_2 te^t $$
- Find the Particular Solution Next, we find a particular solution $y_p(t)$ to the non-homogeneous equation:
$$ y'' - 2y' + y = e^t $$
Assuming a particular solution of the form $y_p(t) = At^2 e^t$, we substitute it into the differential equation and solve for $A$.
- Calculate the Derivatives We compute the first and second derivatives of $y_p(t)$:
- First derivative:
$$ y_p'(t) = e^t(At^2 + 2At) $$
- Second derivative:
$$ y_p''(t) = e^t(At^2 + 4At + 2A) $$
- Substitute Derivatives into the Equation Now substitute $y_p(t)$, $y_p'(t)$, and $y_p''(t)$ back into the equation:
$$ e^t (At^2 + 4At + 2A) - 2e^t (At^2 + 2At) + e^t(At^2) = e^t $$
- Simplify and Solve for A This simplifies to:
$$ e^t( (1 - A)t^2 + (4A - 4A)t + (2A)) = e^t $$
Equate coefficients to find $A$. This leads to:
- From $t^2$: $1 - A = 0$ → $A = 1$
- Constant term gives no additional restrictions.
Thus, the particular solution is:
$$ y_p(t) = t^2 e^t $$
- Complete General Solution The complete solution is:
$$ y(t) = C_1 e^t + C_2 te^t + t^2 e^t $$
- Apply Initial Conditions Using the initial conditions $y(0) = 0$ and $y'(0) = -\frac{1}{2}$ to find constants $C_1$ and $C_2$:
From $y(0) = C_1 + 0 + 0 = 0$, we get $C_1 = 0$.
Now for $y'(t)$:
$$ y'(t) = 0 + C_2 e^t + C_2 te^t + e^t(2t + t^2) $$
Evaluating at $t=0$ gives:
$$ y'(0) = C_2 + 0 + 0 + 0 = -\frac{1}{2} $$
This gives us $C_2 = -\frac{1}{2}$.
- Final Solution and Evaluate y(1) So the final solution is:
$$ y(t) = -\frac{1}{2} te^t + t^2 e^t $$ Now, we can find $y(1)$:
$$ y(1) = -\frac{1}{2} (1)e^1 + (1)^2 e^1 = -\frac{1}{2} e + e = \frac{1}{2} e $$
Finally, approximate $e \approx 2.718$, so:
$$ y(1) \approx \frac{1}{2} \cdot 2.718 \approx 1.359 $$
Rounded to two decimal places, this is:
$$ 1.36 $$
1.36
More Information
The value of the solution at $t=1$ is found from the combined general solution and initial conditions. The result is rounded to two decimal places as required.
Tips
- Failing to correctly apply initial conditions can lead to incorrect constants.
- Not simplifying coefficients properly can cause errors in the final answer.
AI-generated content may contain errors. Please verify critical information