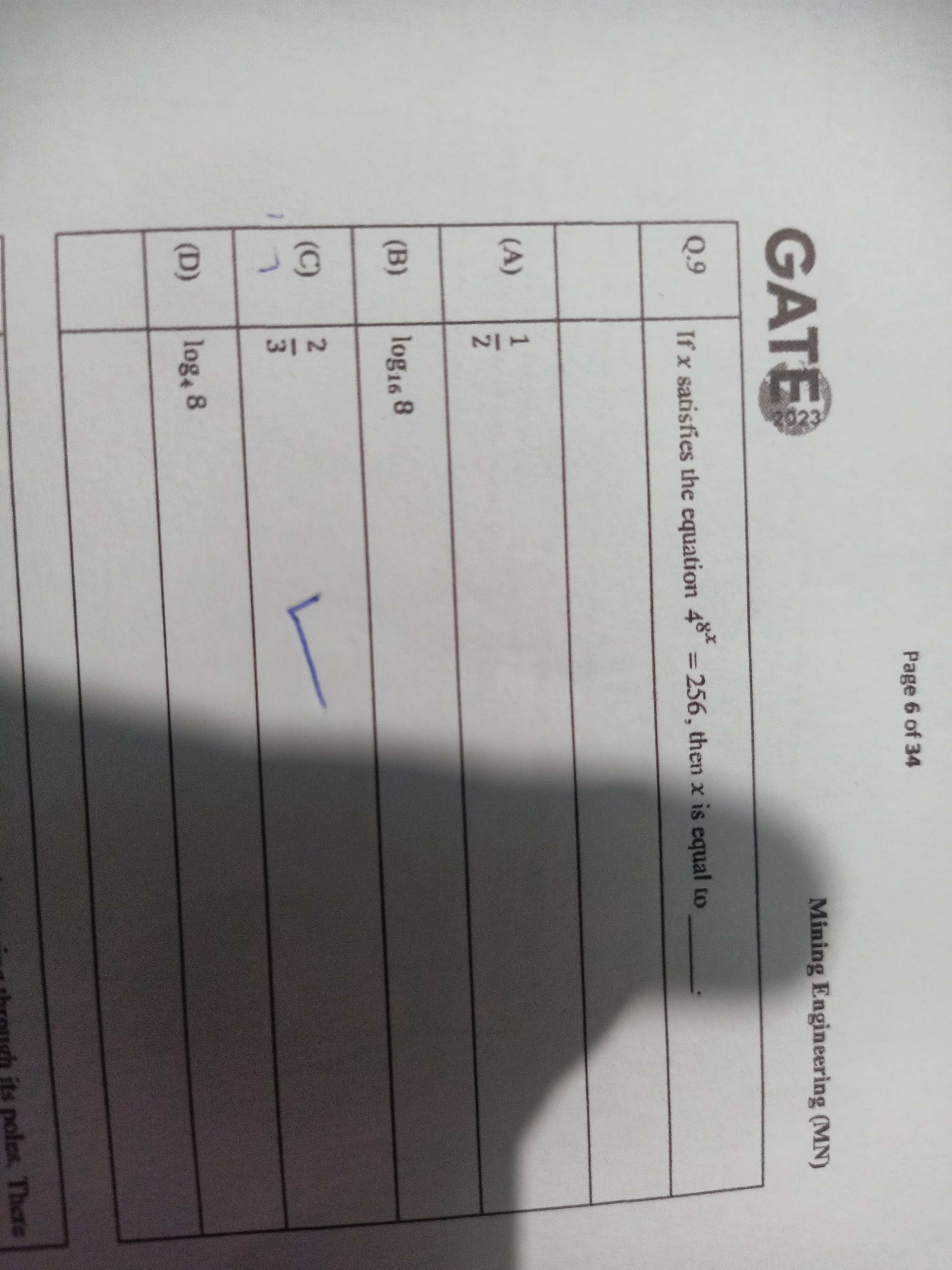
If x satisfies the equation 4^x = 256, then x is equal to __.
Understand the Problem
The question is asking to solve for 'x' in the equation 4^x = 256, which can be approached by expressing 256 as a power of 4.
Answer
The value of \( x \) is \( 4 \).
Answer for screen readers
The value of ( x ) is ( 4 ).
Steps to Solve
- Express 256 as a Power of 4
First, we need to rewrite 256 in terms of the base 4. We know that: $$ 256 = 4^4 $$
- Set the Exponents Equal
Now that we have both sides of the equation in terms of base 4, we can set the exponents equal: $$ x = 4 $$
- Evaluate the Result
Thus, we find that: $$ x = 4 $$
The value of ( x ) is ( 4 ).
More Information
Since ( 4^4 = 256 ), we confirmed that our solution is correct by converting back to check if both sides of the equation equal.
Tips
- Miscalculating the power of 4 or 256 can lead to incorrect results. It's essential to accurately express numbers in their exponential forms before solving.
AI-generated content may contain errors. Please verify critical information
Thank you for voting!
