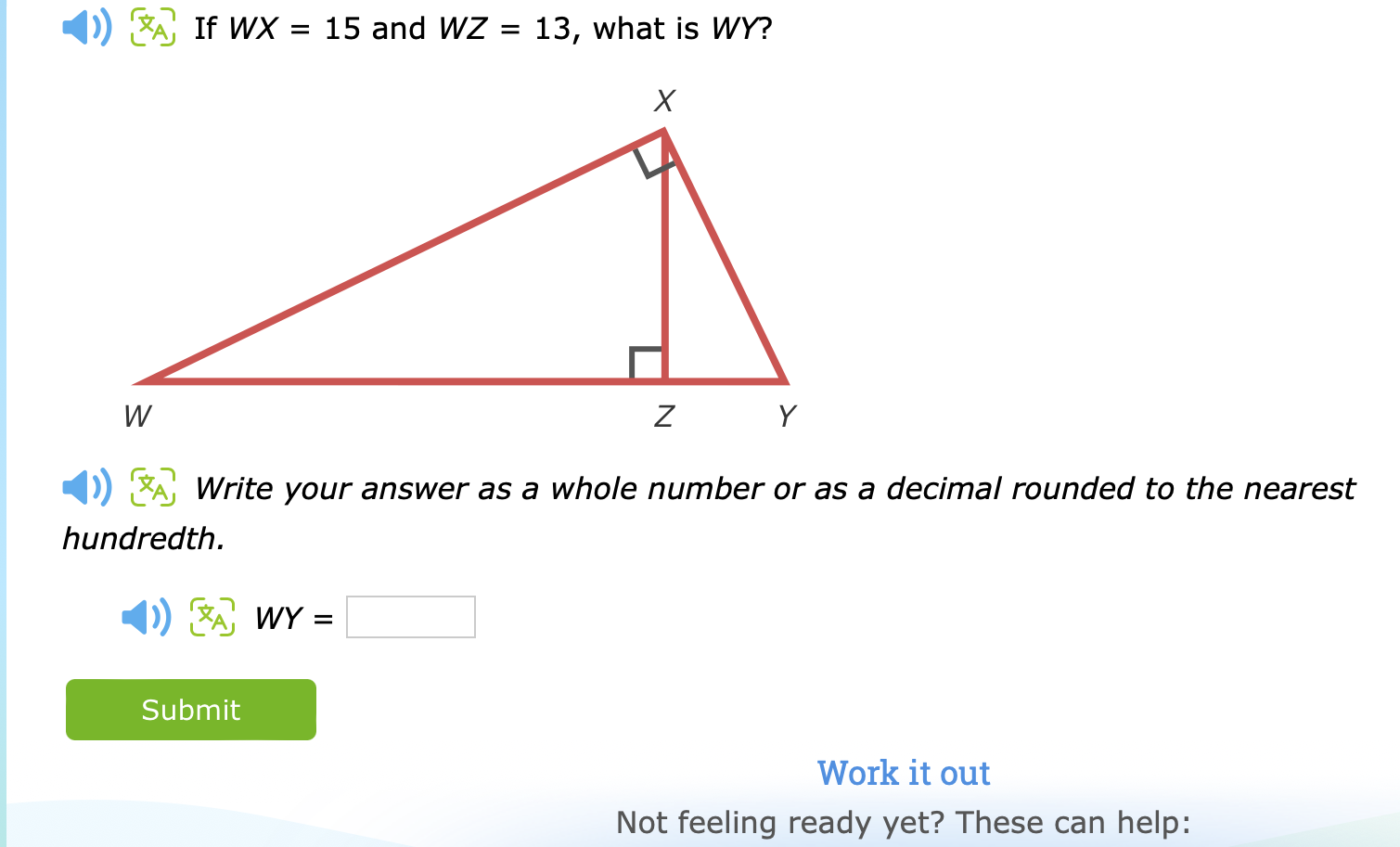
If WX = 15 and WZ = 13, what is WY?
Understand the Problem
The question is asking to find the length of side WY in a right triangle, given the lengths of sides WX and WZ. This involves using the Pythagorean theorem since it is a right triangle.
Answer
$WY \approx 19.85$
Answer for screen readers
$WY \approx 19.85$
Steps to Solve
- Identify the Known Values
We have the lengths of two sides of the triangle:
- $WX = 15$ (one leg)
- $WZ = 13$ (the other leg)
- Apply the Pythagorean Theorem
In a right triangle, the Pythagorean theorem states:
$$ a^2 + b^2 = c^2 $$
where $c$ is the hypotenuse and $a$, $b$ are the legs. Here, we can take:
- $a = WX = 15$
- $b = WZ = 13$
- Substitute the Known Values into the Equation
We substitute the values into the equation:
$$ 15^2 + 13^2 = WY^2 $$
- Calculate Each Square
Calculate the squares:
$$ 15^2 = 225 $$
$$ 13^2 = 169 $$
- Add the Squares
Now, we add the two results together:
$$ 225 + 169 = WY^2 $$
$$ 394 = WY^2 $$
- Take the Square Root
To find $WY$, we take the square root of both sides:
$$ WY = \sqrt{394} $$
- Calculate the Square Root
Using a calculator, compute the square root:
$$ WY \approx 19.85 $$
$WY \approx 19.85$
More Information
The value of $WY$ calculated is approximately 19.85. This corresponds to the length of the side opposite the right angle in the triangle when the other two sides are known.
Tips
- Not Using the Pythagorean Theorem: Some may forget to apply the theorem correctly for right triangles.
- Miscalculating Squared Values: Ensure that the squares of the sides are calculated accurately.
AI-generated content may contain errors. Please verify critical information