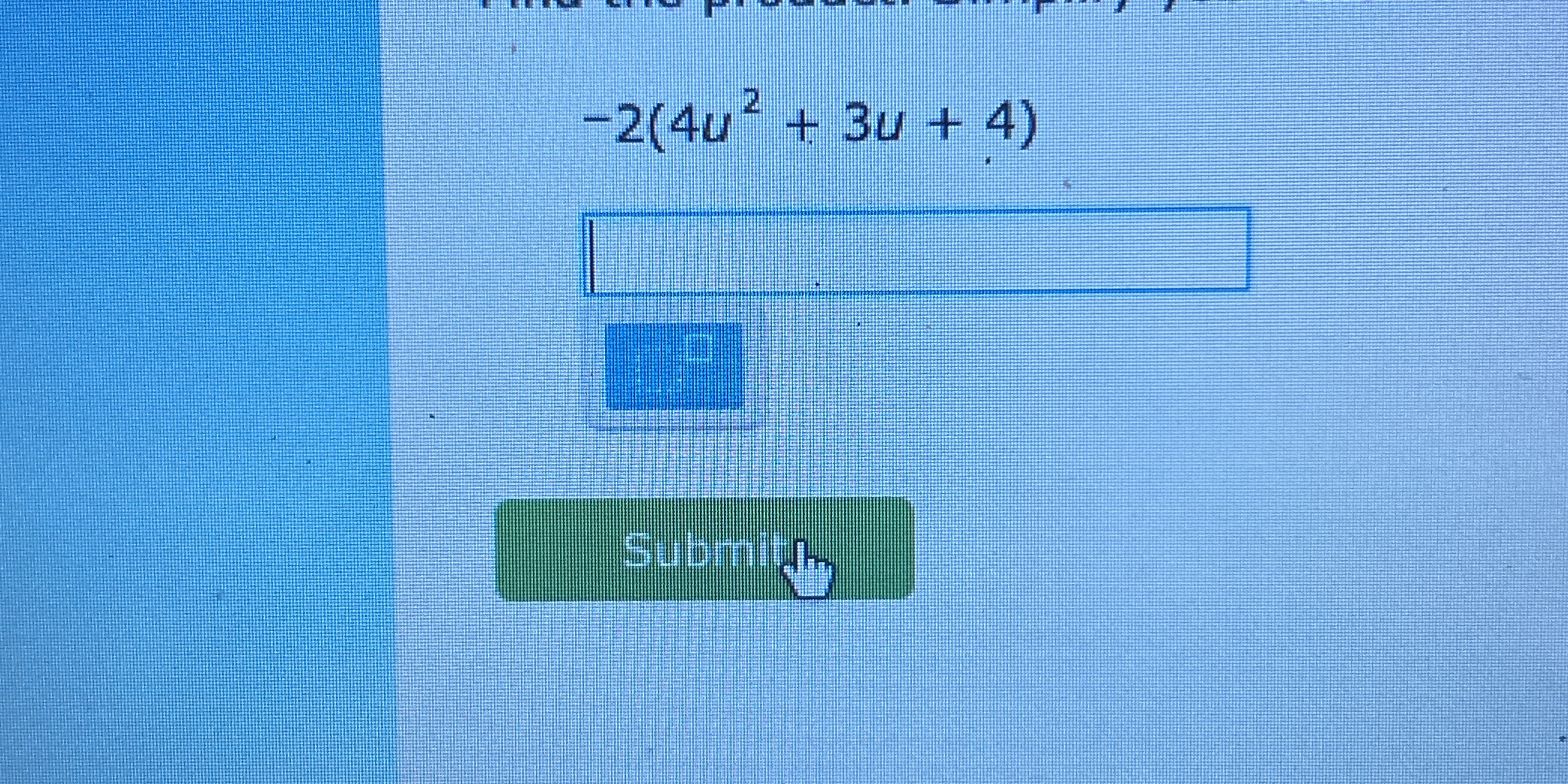
Find the product of -2(4u² + 3u + 4).
Understand the Problem
The question is asking to find the product of the expression -2(4u² + 3u + 4). To solve this, we will distribute -2 to each term inside the parentheses.
Answer
The simplified product is: $-8u^2 - 6u - 8$
Answer for screen readers
The simplified product is:
$$ -8u^2 - 6u - 8 $$
Steps to Solve
- Distribute -2 to the first term
Multiply -2 by the first term in the parentheses:
$$ -2 \cdot 4u^2 = -8u^2 $$
- Distribute -2 to the second term
Multiply -2 by the second term in the parentheses:
$$ -2 \cdot 3u = -6u $$
- Distribute -2 to the third term
Multiply -2 by the third term in the parentheses:
$$ -2 \cdot 4 = -8 $$
- Combine the results
Now combine all the distributed terms:
$$ -8u^2 - 6u - 8 $$
The simplified product is:
$$ -8u^2 - 6u - 8 $$
More Information
This result represents a quadratic expression that has been factored out by -2. Quadratic expressions are common in algebra and appear frequently in problem-solving.
Tips
- Failing to distribute the negative sign correctly, resulting in incorrect signs for the terms.
- Forgetting to multiply each term in the parentheses.
AI-generated content may contain errors. Please verify critical information