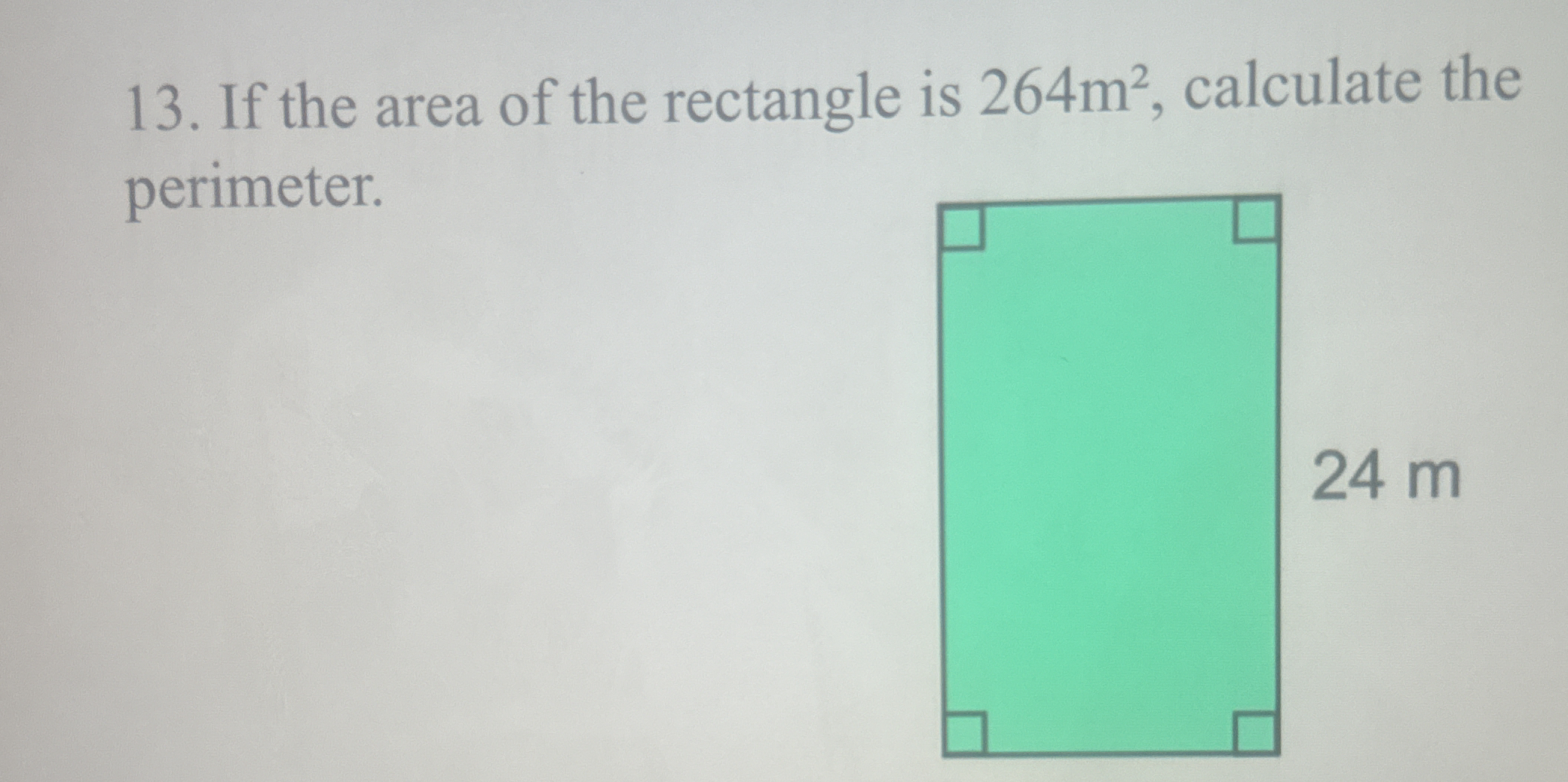
If the area of the rectangle is 264 m², calculate the perimeter.
Understand the Problem
The question is asking for the perimeter of a rectangle given the area and one of its dimensions. We need to use the area formula (Area = length × width) to find the missing dimension and then use the perimeter formula (Perimeter = 2 × (length + width)) to calculate the perimeter.
Answer
The perimeter of the rectangle is $70 \, m$.
Answer for screen readers
The perimeter of the rectangle is $70 , m$.
Steps to Solve
-
Identify known values The area of the rectangle is given as $264 , m^2$, and one dimension (length) is $24 , m$.
-
Use the area formula The area of a rectangle is calculated using the formula: $$ \text{Area} = \text{length} \times \text{width} $$ Substituting the known values: $$ 264 = 24 \times \text{width} $$
-
Solve for the width To find the width, rearrange the equation: $$ \text{width} = \frac{264}{24} $$ Calculating the width: $$ \text{width} = 11 , m $$
-
Use the perimeter formula The perimeter of a rectangle is given by: $$ \text{Perimeter} = 2 \times (\text{length} + \text{width}) $$ Substituting the known values: $$ \text{Perimeter} = 2 \times (24 + 11) $$
-
Calculate the perimeter Now, perform the calculations: $$ \text{Perimeter} = 2 \times 35 = 70 , m $$
The perimeter of the rectangle is $70 , m$.
More Information
The perimeter is the total distance around a rectangle. Knowing one side and the area allows us to calculate the missing side effectively, leading to the final calculation of the perimeter.
Tips
- Confusing area and perimeter; it's essential to use the correct formulas.
- Incorrectly rearranging the area formula; make sure to divide the area by the known dimension correctly.
AI-generated content may contain errors. Please verify critical information